Calculateur de Pente en Ligne - Nos 8 Outils Gratuits
Notre suite complète de calculs de pente va vous permettre de calculer une pente que ce soit en pourcentage, en degrés, en radians, mais également dans toutes les unités d'angle et de pente existantes. Que vous ayez besoin de calculer la pente de votre toit, d'une rampe pour l'accès PMR, de votre terrain ou d'une route en particulier, nos outils couvrent un grand spectre de cas d'usage. Aucune inscription, le calcul s'effectue 100% côté client, donc dans votre navigateur, vos données restent privées.
Nos 8 modules de calcul
Le calculateur de pente de base
Il permet le calcul de pente depuis la hauteur et la distance horizontale, ou directement depuis un angle si vous le connaissez. Vous entrez votre dénivelé et la distance parcourue pour obtenir le pourcentage de pente ainsi que l'angle en degrés, en radians, le ratio et la longueur d'hypoténuse.
La formule qui sera utilisée est relativement simple, il s'agit de la pente en pourcentage qui est égale à la hauteur sur la distance horizontale multipliée par 100 : Pente (%) = (Hauteur / Distance horizontale) × 100. Concernant l'angle θ : θ = arctan(Hauteur / Distance). Le calculateur catégorisera automatiquement la pente, il la classifie de très douce à extrême avec des exemples d'applications concrètes.
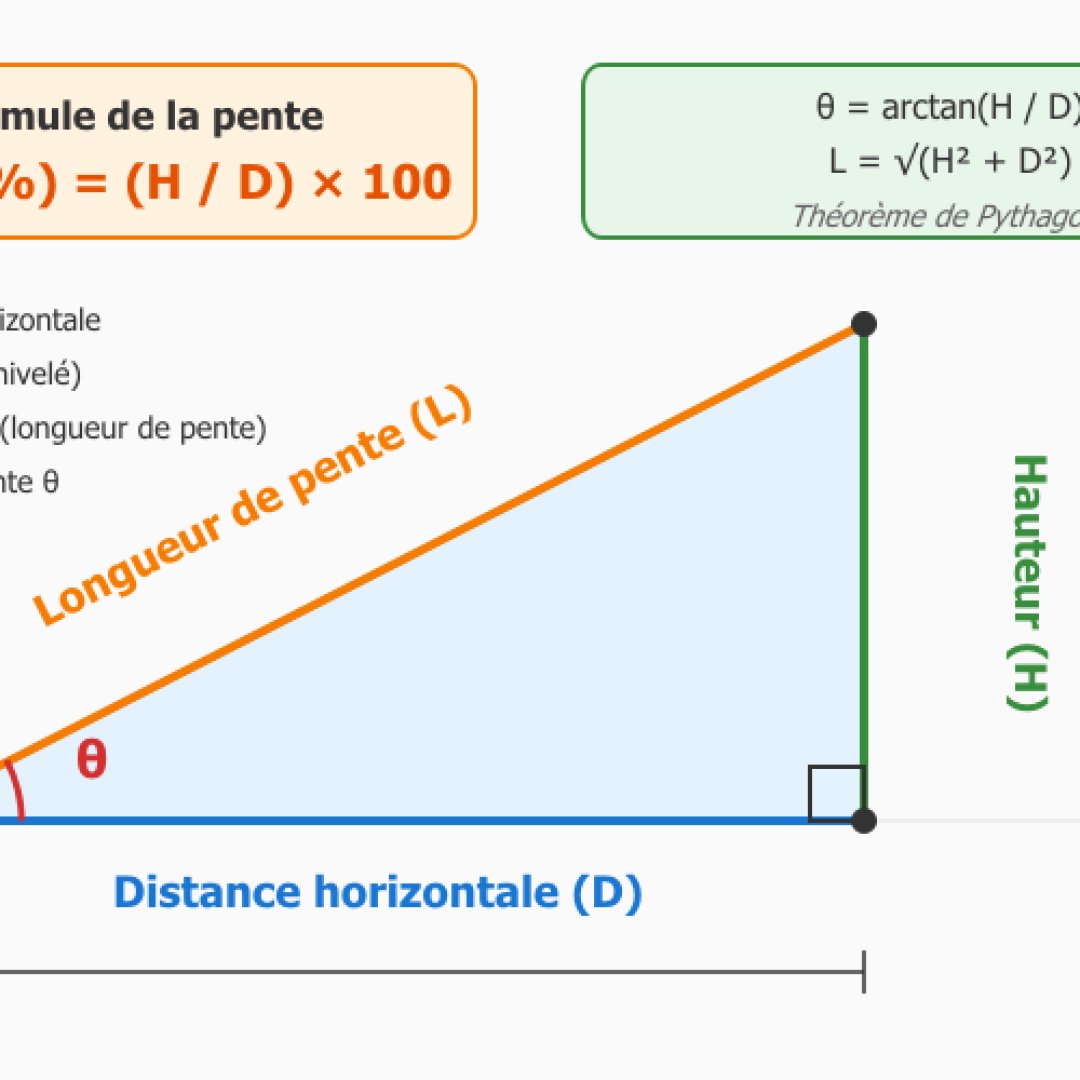
Ce module vous permet également de faire le calcul inverse. C'est à dire, à partir d'un angle connu et d'une dimension (distance horizontale, hauteur ou hypoténuse), il va déterminer les deux autres dimensions qui sont manquantes grâce aux relations trigonométriques fondamentales.
Le convertisseur d'unité angulaire
Le convertisseur d'unité angulaire est complet et vous permet de passer d'une unité à l'autre en direct. Il supporte 10 types d'unités, que ce soit le pourcentage, le degré, les radians, gradians (utilisés en topographie), les tours (utilisés par exemple en CSS), les milliradians (balistique), les mils NATO (militaire), les minutes d'arc et secondes d'arc (astronomie), et le ratio (1:X).
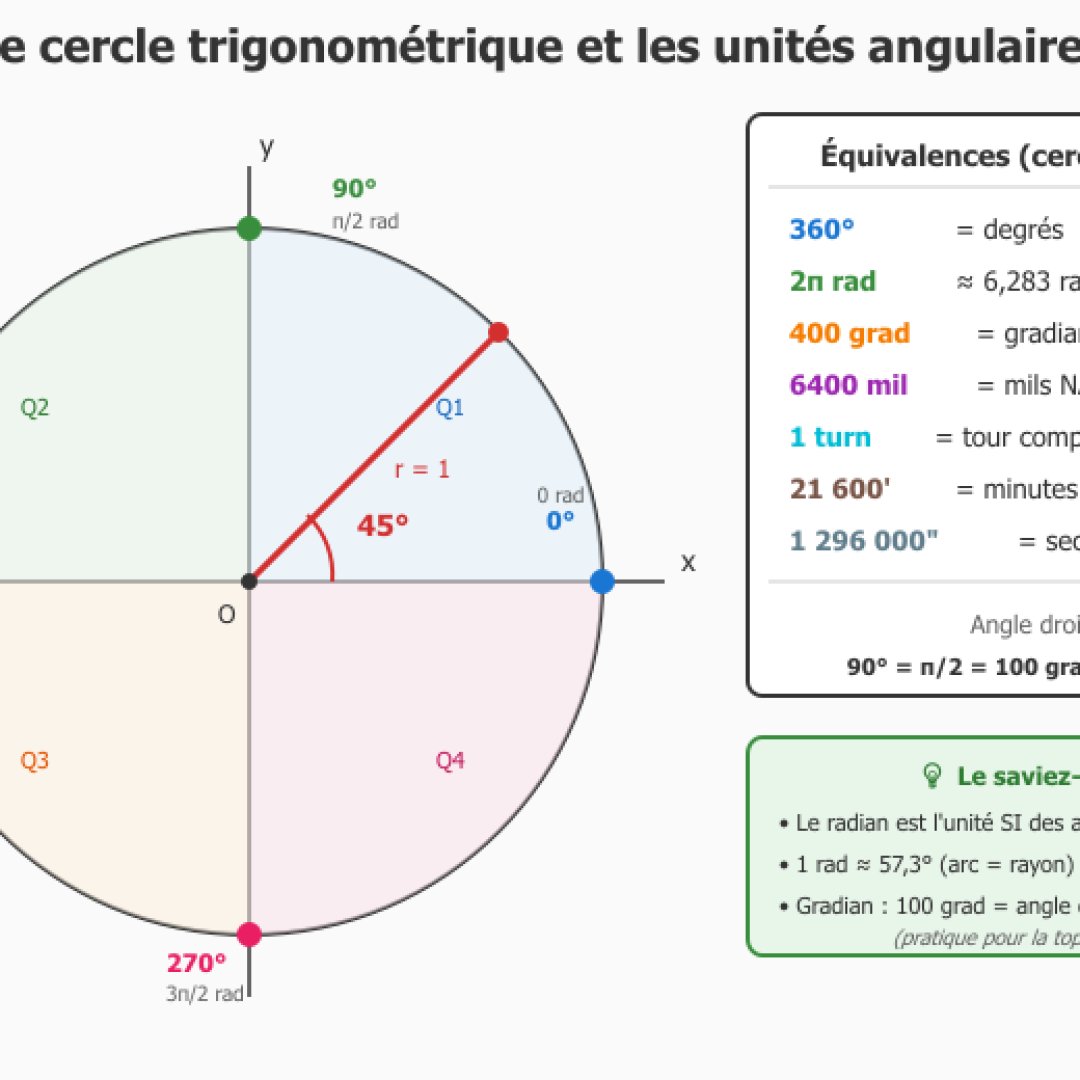
La visualisation dynamique vous affichera le cercle trigonométrique ainsi que le triangle de pente pour comprendre visuellement la relation qui existe entre l'angle et l'inclinaison. Les angles remarquables sont detectés automatiquement ( normalement ^^ ) et affiche leur notation en π (par exemple π/4 rad pour 45°).
Le calcul de distance et point milieu
Ce module permet de calculer la distance euclidienne entre deux points en deux dimensions ou en trois dimensions. Concernant le calcul trois dimensions, il détermine également la pente du terrain entre deux altitudes, ce qui peut être utile en topographie ainsi qu'en randonnée.
Les formules sont basées sur le théorème de Pythagore, démontré dans les Éléments d'Euclide (Livre I, Proposition 47) :
- Distance 2D = √[(x₂-x₁)² + (y₂-y₁)²]
- Distance 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]
- Point milieu = ((x₁+x₂)/2, (y₁+y₂)/2)
Le module 3D calcule aussi les angles directeurs du vecteur déplacement par rapport aux trois axes X, Y et Z, ce qui peut utile en topographie et en navigation mais à vrai dire c'est surtout utile à l'école !
Équation de ligne (y = mx + b)
Permet de générer l'équation d'une droite à partir de deux points ou d'une pente et d'un point. Ce module fournit trois types de formes : la pente-ordonnée (y = mx + b), le point-pente (y - y₁ = m(x - x₁)) ainsi que la forme standard (Ax + By = C). Il vous permet de calculer l'abscisse à l'origine, l'ordonnée à l'origine et de vérifier si trois points sont colinéaires en toute simplicité.
La colinéarité sera vérifiée par le calcul de l'aire du triangle formé par les trois points. Si l'aire est nulle, les points sont alors alignés.
La visualisation graphique interactive
En utilisant un graphique avec la librairie Chart.js, il permet de tracer vos lignes et points. Vous ajoutez des lignes par équation ou coordonnées. Vous contrôlez le zoom de ±5 à ±100. Vous activez et désactivez les grilles. Et vous pouvez exporter le résultat soit en image PNG ou en format vectoriel SVG qui permet de ne pas perdre en qualité à l'agrandissement.
Lignes parallèles et perpendiculaires
Vous permettent de trouver l'équation d'une droite parallèle ou perpendiculaire passant par un point donné. Les règles mathématiques sont les suivantes : deux lignes sont parallèles si m₁ = m₂, perpendiculaires si m₁ × m₂ = -1. Le vérificateur intégré analyse la relation existante entre deux pentes et calcule l'angle formé entre deux droites sécantes.
Ces propriétés découlent directement de la géométrie euclidienne, notions fondamentales en géométrie analytique pour l'étude des droites dans le plan cartésien.
Régression linéaire
Vous permettra de calculer la ligne de tendance par la méthode des moindres carrés en saisissant vos données manuellement, soit en les collant ou en les important grâce à un fichier CSV. Le module va calculer le coefficient de corrélation R, le coefficient de détermination R² ainsi que l'erreur standard et les résidus. Ainsi, vous pouvez faire des prédictions de Y pour X donné.
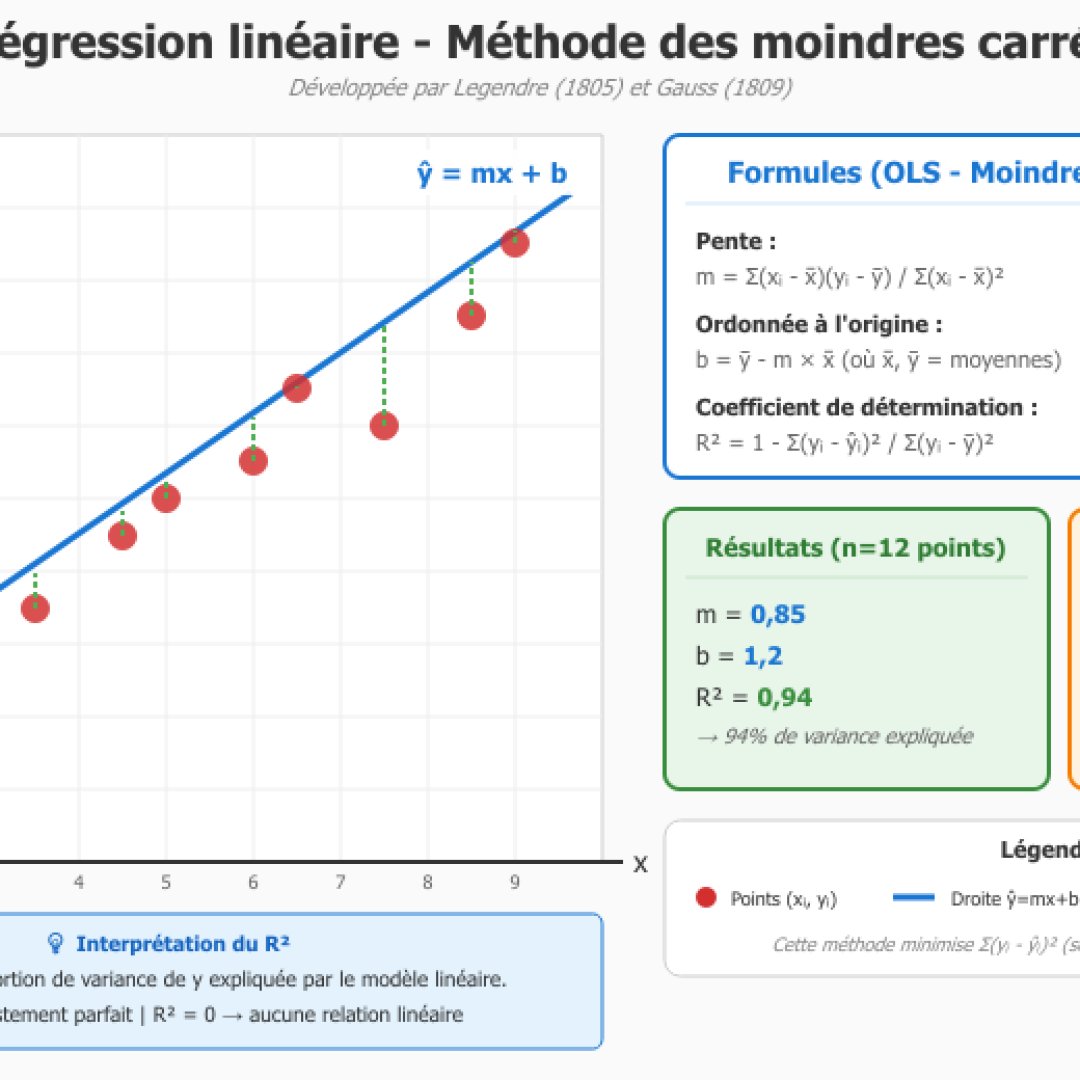
La méthode des moindres carrés a été développée par Adrien-Marie Legendre (1805) et Carl Friedrich Gauss (1809), elle minimise la somme des carrés des écarts entre les valeurs observées et les valeurs prédites par le modèle linéaire.
Angles et élévation
Vous calculez les angles d'élévation et de dépression pour vos projets, que ce soit par exemple dans le cadre du tir balistique, du pointage de vos télescopes vers les étoiles, pour calculer un angle de montée en avion ou le calcul d'une pente de rampe pour vos activités de construction. Le calcul inverse permet de trouver la distance ou la hauteur manquante à partir d'un angle connu.
Ce module accepte l'angle d'entrée dans les 10 unités supportées, y compris directement en pourcentage de pente.
Comprendre simplement le calcul de pente
La pente en pourcentage
Le pourcentage de pente va représenter le rapport qui existe entre le dénivelé et la distance horizontale, le tout multiplié par 100. Une pente de 10% va alors signifier que pour 100 mètres de distance horizontale, vous gagnerez 10 mètres d'élévation. C'est le format standard qui est utilisé sur les panneaux routiers et en construction.
La pente en degré
L'angle de la pente va mesurer l'inclinaison par rapport à l'horizontale. Ainsi, un angle de 45 degrés correspond à une pente de 100% (hauteur égale distance). La conversion utilise la fonction tangente : % = tan(angle) × 100.
Correspondances courantes
| Pourcentage | Angle | Usage typique |
|---|---|---|
| 5% | 2.9° | Rampe PMR (maximum légal) |
| 10% | 5.7° | Piste cyclable, allée |
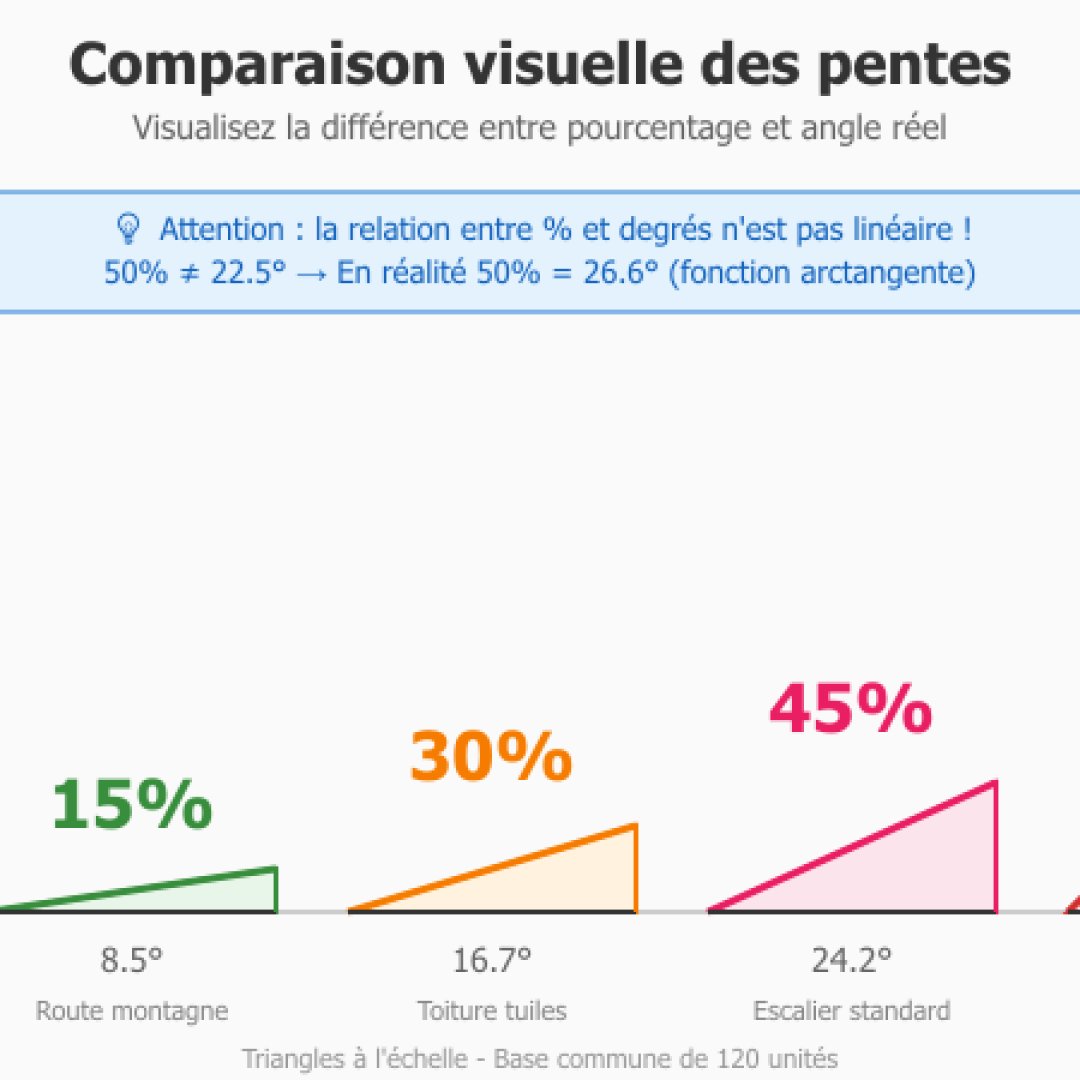
| 15% | 8.5° | Route de montagne |
| 30% | 16.7° | Escalier doux, toiture faible pente |
| 45% | 24.2° | Escalier standard |
| 100% | 45° | Pente maximale praticable |
Applications pratiques
Calcul de pente de toiture
La pente du toit influence nécessairement le choix des matériaux de couverture ainsi que l'écoulement des eaux de pluie. Les toitures terrasses nécessitent en général un 5% minimum pour assurer l'évacuation des eaux de pluie. Les toits en tuiles demandent généralement 15 à 35% selon le type de tuile (tuiles mécaniques, tuiles canal ou ardoises). Les zones de montagne enneigées requièrent des pentes plus fortes de 35% à 60% pour éviter que les toits ne s'effondrent en hiver sous le poids de la neige.
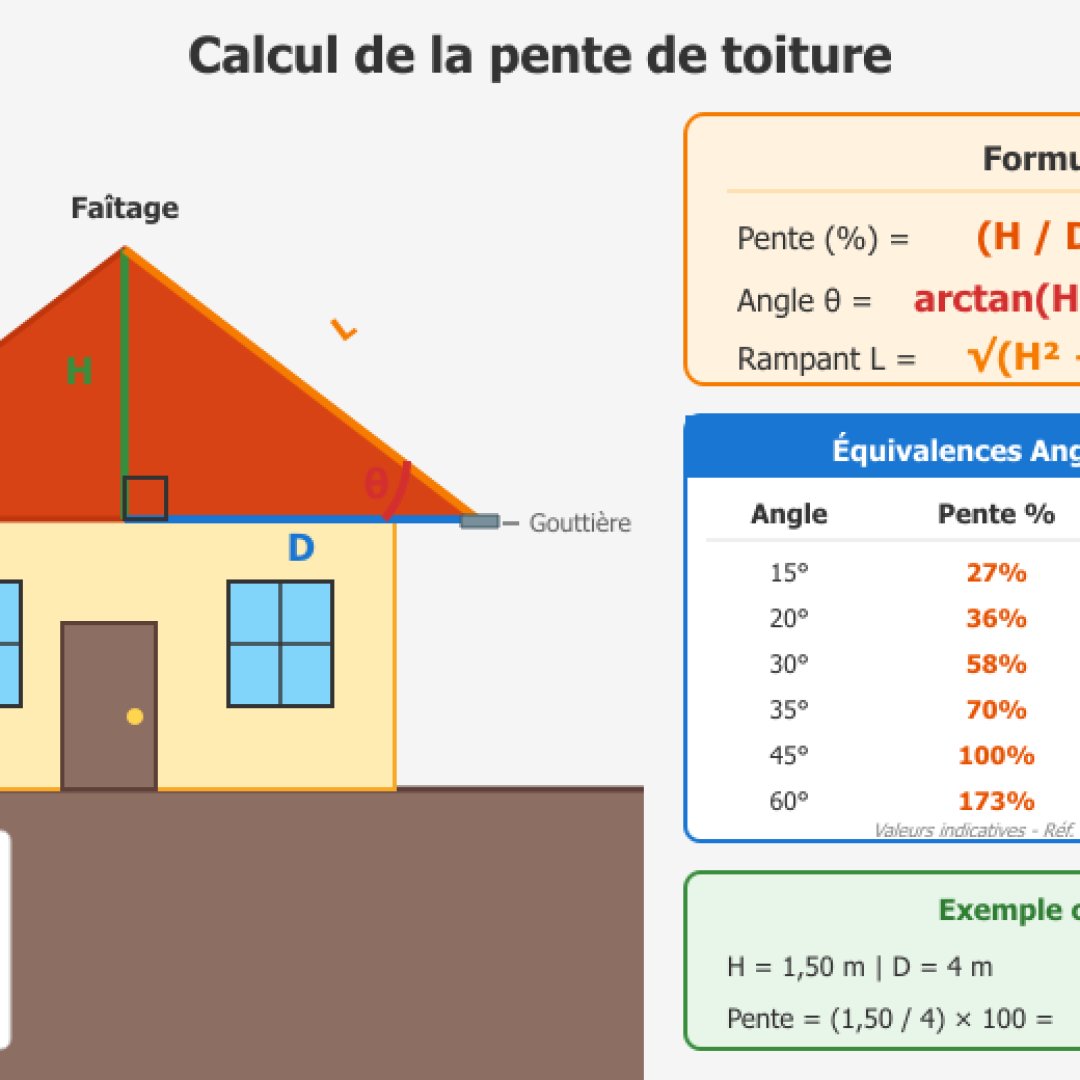
Ainsi, pour calculer la pente de votre toit, vous devez mesurer la hauteur du pignon et la distance horizontale (la demi-largeur du bâtiment pour un toit qui est à deux pans). Notre petit calculateur de pente de toiture donne le résultat en pourcentage et en degré.
La rampe pour les personnes à mobilité réduite (PMR) et accessibilité
La réglementation française va imposer une pente maximale de 5% pour les rampes d'accès PMR (personnes à mobilité réduite). Néanmoins, des dérogations permettent jusqu'à 8% sur 2 mètres au maximum ou 10% sur 50 cm. Notre calculateur permettra de vérifier la conformité de votre projet d'amélioration de l'accessibilité PMR.
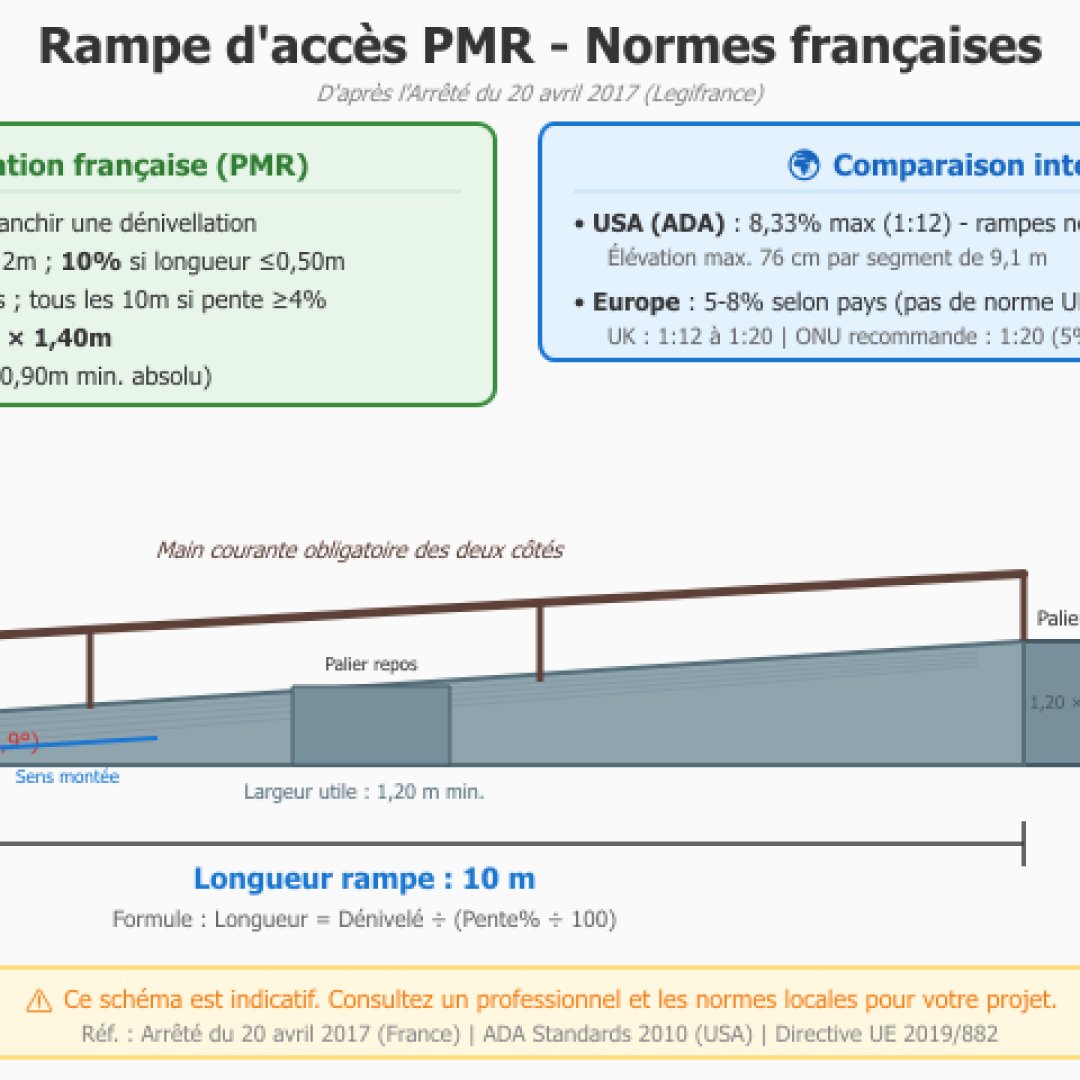
Référence : Arrêté du 20 avril 2017 relatif à l'accessibilité aux personnes handicapées des établissements recevant du public.
À titre de comparaison, la réglementation américaine ADA (Americans with Disabilities Act) impose également un ratio maximum de 1:12 (soit 8.33%) pour les rampes d'accès public.
Topographie et terrain
Il faut savoir qu'en topographie, la pente va se calculer entre deux points de mesure à différentes altitudes. Les courbes de niveau sur les cartes IGN permettent de déterminer le dénivelé (l'équidistance est égale à la différence d'altitude entre deux courbes de niveau). Notre petit module va calculer la pente réelle du terrain en tenant compte de l'altitude.
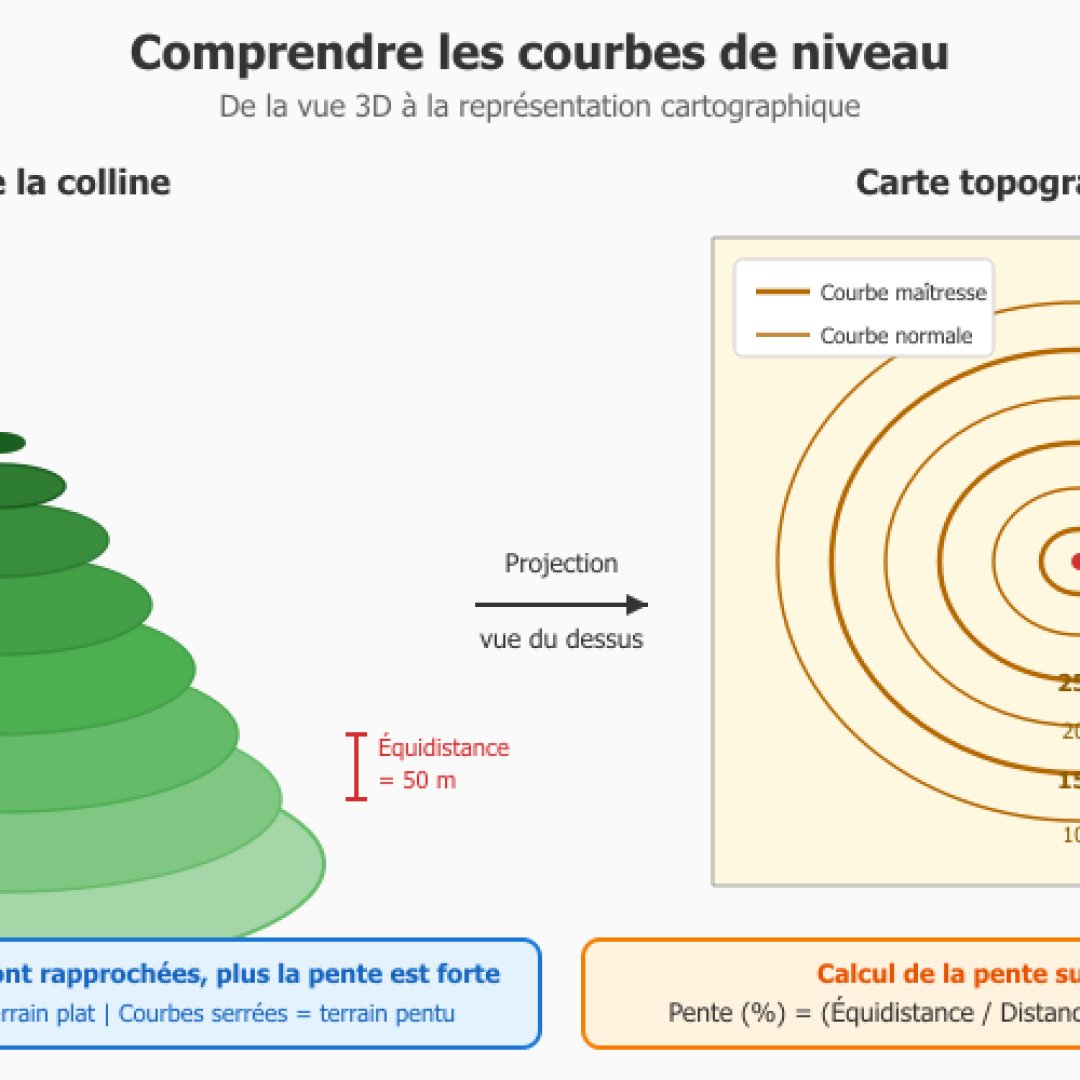
En topographie professionnelle, l'unité gradian (ou gon) est souvent préférée car elle divise le cercle en 400 parties, ce qui simplifie les calculs (un angle droit = 100 grad exactement), en revanche dans le cadre militaire on s'exprime frequement en millieme dans l'armée de terre et plus en degrés au niveau OTAN.
Charpente et construction
Le calcul de votre charpente bois va dépendre de la pente choisie. Une toiture constituée d'un pan ou de deux pentes nécessite des chevrons qui seront dimensionnés selon l'inclinaison et la portée. La longueur de la pente (qui correspond à l'hypoténuse) va déterminer la quantité de matériaux de couverture nécessaires pour votre projet.
Formules de référence
Calcul du pourcentage de pente
Pente (%) = (Hauteur / Distance horizontale) × 100Conversion pourcentage vers degrés
Angle (°) = arctan(Pente% / 100) × (180 / π)Conversion degrés vers radians
Radians = Degrés × (π / 180)Longueur de la pente (théorème de Pythagore)
Longueur = √(Hauteur² + Distance²)Relations trigonométriques
tan(angle) = Hauteur / Distance = Pente% / 100
sin(angle) = Hauteur / Hypoténuse
cos(angle) = Distance / HypoténuseConversions d'unités angulaires
Gradians = Degrés × (400 / 360)
Mils NATO = Degrés × (6400 / 360)
Minutes d'arc = Degrés × 60
Secondes d'arc = Degrés × 3600
Tours = Degrés / 360
Milliradians = Radians × 1000Équation de droite
Forme pente-ordonnée : y = mx + b
Forme point-pente : y - y₁ = m(x - x₁)
Forme standard : Ax + By = CRégression linéaire (méthode des moindres carrés)
Pente (m) = [n∑xy - ∑x∑y] / [n∑x² - (∑x)²]
Ordonnée (b) = ȳ - m × x̄
Coefficient R² = 1 - [∑(y - ŷ)² / ∑(y - ȳ)²]Distance euclidienne
Distance 2D = √[(x₂-x₁)² + (y₂-y₁)²]
Distance 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]Lignes parallèles et perpendiculaires
Parallèles : m₁ = m₂
Perpendiculaires : m₁ × m₂ = -1Unités angulaires : guide de référence
| Unité | Symbole | Cercle complet | Usage principal |
|---|---|---|---|
| Degré | ° | 360° | Géométrie, construction, navigation |
| Radian | rad | 2π ≈ 6.283 | Mathématiques, physique, ingénierie |
| Gradian | grad | 400 grad | Topographie, géodésie (Europe) |
| Tour | turn | 1 turn | Programmation (CSS), robotique |
| Milliradian | mrad | ~6283 mrad | Balistique, optique, lunettes de tir |
| Mil NATO | mil | 6400 mil | Applications militaires OTAN |
| Minute d'arc | ′ | 21 600′ | Astronomie, navigation maritime |
| Seconde d'arc | ″ | 1 296 000″ | Haute précision, coordonnées GPS |
Le radian est l'unité d'angle du Système International (SI), défini par le BIPM dans la Brochure SI. Il correspond à l'angle au centre qui intercepte un arc de longueur égale au rayon du cercle ( Imagine un cercle : c'est l'angle au centre qui découpe un arc (une portion de la circonférence) exactement de la même longueur que le rayon du cercle. C'est comme si tu déroulais le rayon le long du bord du cercle pour former cet angle de base !).
Questions fréquentes
Comment calculer une pente en pourcentage ?
Vous divisez simplement la hauteur (dénivelé) par la distance horizontale. Puis vous multipliez le tout par 100. Par exemple, 5 mètres de dénivelé sur 50 mètres de distance correspondra à 10% de pente. Notre outil vous permet de faire ce calcul automatiquement.
Quelle est la différence entre un pourcentage et les degrés ?
D'un côté le pourcentage va représenter un ratio qui correspond à la hauteur divisée par la distance multipliée par 100, et les degrés eux vont mesurer l'angle géométrique. La relation n'est pas linéaire. C'est-à-dire que 100% est égal à 45 degrés. Mais 50% ne sera pas 22,5 degrés. En réalité c'est 26,6 degrés. Cette non-linéarité provient de la fonction arctangente ( parfait pour briller en société ) utilisée pour la conversion.
Comment faire pour calculer la pente d'un toit ?
Vous devez mesurer la hauteur du faîtage depuis le niveau des gouttières et la distance horizontale jusqu'au point de mesure. Ensuite, utilisez notre calculateur de pente de toiture pour obtenir le pourcentage et vérifier la compatibilité avec votre revêtement, que ce soit des tuiles, des ardoises ou des tôles.
Quelle pente pour une toiture bac acier ?
Le bac acier accepte des pentes qui sont plus faibles, généralement à partir de 5% (3 degrés), selon les recommandations DTU. Les pentes inférieures nécessitent une étanchéité renforcée pour votre projet.
Référence : NF DTU 40.35 - Couverture en plaques nervurées issues de tôles d'acier revêtues (AFNOR).
Comment mesurer une pente sur le terrain ?
Tout simplement. Si vous en êtes équipé, utilisez un niveau laser rotatif, un clinomètre ou une application smartphone avec un accéléromètre. Et pour les grandes distances, vous relevez l'altitude à deux points, soit avec un système GPS qui vous permet de faire un relevé altimétrique, ou tout simplement vous le calculez à partir de votre position depuis une carte topographique. Et vous mesurez la distance horizontale parcourue.
Qu'est-ce que le coefficient R² en régression linéaire ?
Le coefficient de détermination R² indique la proportion de la variance des données qui est expliquée par le modèle linéaire. Un R² de 0.95 signifie que 95% de la variation des données est expliquée par la droite de régression. Plus R² est proche de 1, meilleur est l'ajustement du modèle.
Pourquoi utiliser notre calculateur ?
Notre suite de calculs de pente vous offre 8 modules qui sont complémentaires, qui couvrent un maximum des besoins existants, que ce soit du simple calcul de pourcentage jusqu'à la régression linéaire avancée qui fait mal à la tête. L'interface vous permet de réaliser vos calculs simplement depuis votre téléphone mobile, votre tablette ou votre ordinateur. Sachez que tous les calculs s'effectuent depuis votre navigateur, pour un maximum de rapidité et garantir une confidentialité totale des données que vous soumettez.
Nous avons essayé de mettre un maximum d'unités angulaires disponibles pour tous, au même endroit (degrés, radians, gradians, pourcentages, ratios, milliradians, mils NATO, minutes et secondes d'arc et les tours). Normalement, ils répondent aux besoins des professionnels de la construction, de la topographie, balistique, astronomie et des élèves studieux.
Calculez votre pente maintenant avec nos outils gratuits.