Calculadora de Declive Online - Nossas 8 Ferramentas Gratuitas
Nossa suíte completa de cálculos de declive permitirá que você calcule um declive seja em porcentagem, em graus, em radianos, mas também em todas as unidades de ângulo e declive existentes. Seja você precisando calcular o declive do seu telhado, de uma rampa para acesso PMR, do seu terreno ou de uma estrada em particular, nossas ferramentas cobrem um amplo espectro de casos de uso. Sem necessidade de registro, o cálculo é feito 100% no lado do cliente, portanto no seu navegador, seus dados permanecem privados.
Nossos 8 módulos de cálculo
A calculadora de declive básica
Ela permite o cálculo de declive a partir da altura e da distância horizontal, ou diretamente a partir de um ângulo se você o conhece. Você insere seu desnível e a distância percorrida para obter a porcentagem de declive assim como o ângulo em graus, em radianos, a razão e o comprimento da hipotenusa.
A fórmula que será usada é relativamente simples, trata-se do declive em porcentagem que é igual à altura sobre a distância horizontal multiplicada por 100: Declive (%) = (Altura / Distância horizontal) × 100. Quanto ao ângulo θ: θ = arctan(Altura / Distância). A calculadora categorizará automaticamente o declive, classificando-o de muito suave a extremo com exemplos de aplicações concretas.
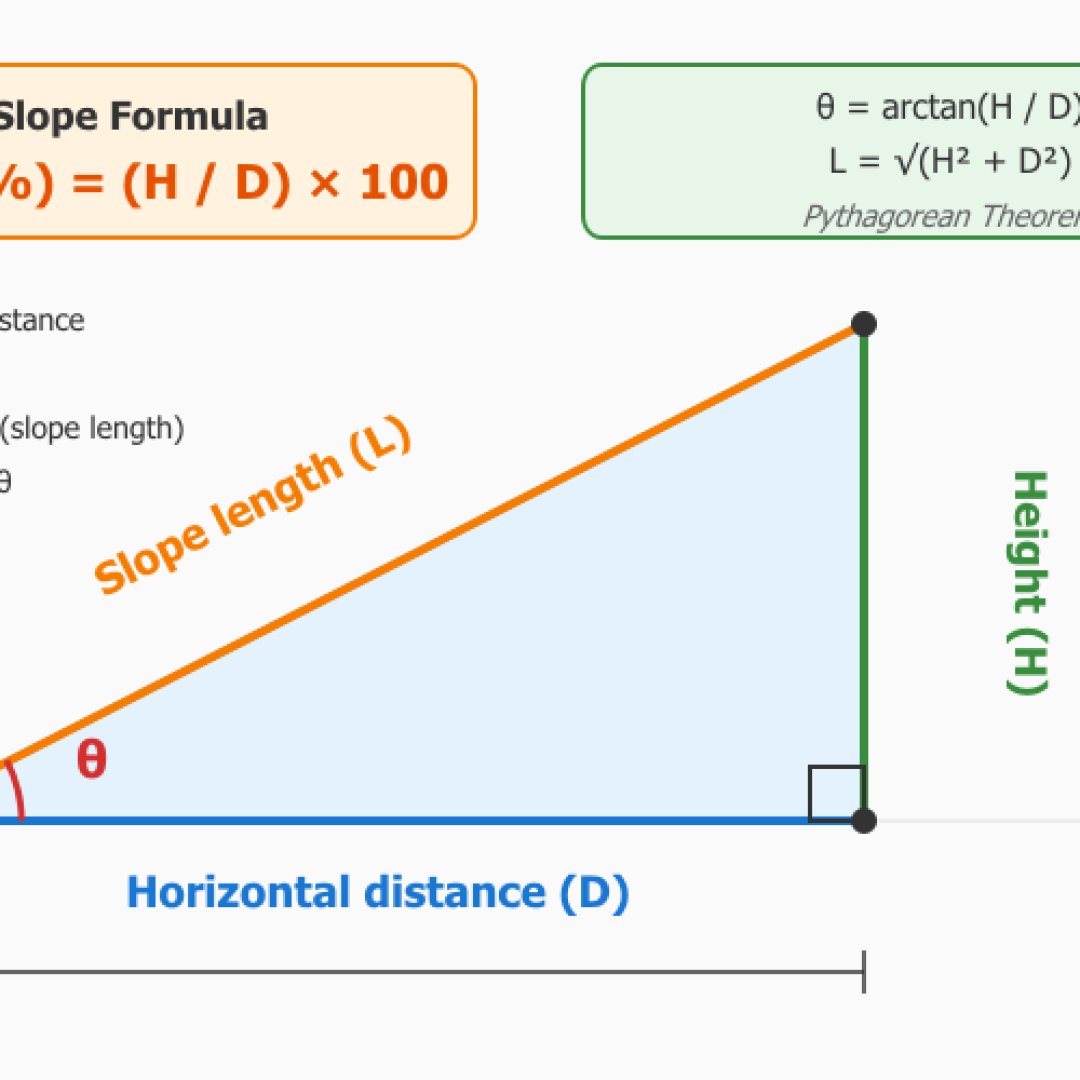
Este módulo também permite fazer o cálculo inverso. Ou seja, a partir de um ângulo conhecido e de uma dimensão (distância horizontal, altura ou hipotenusa), ele determinará as duas outras dimensões que estão faltando graças às relações trigonométricas fundamentais.
O conversor de unidade angular
O conversor de unidade angular é completo e permite passar de uma unidade para outra em tempo real. Ele suporta 10 tipos de unidades, seja a porcentagem, o grau, os radianos, gradianos (usados em topografia), as voltas (usadas por exemplo em CSS), os miliradianos (balística), os mils NATO (militar), os minutos de arco e segundos de arco (astronomia), e a razão (1:X).
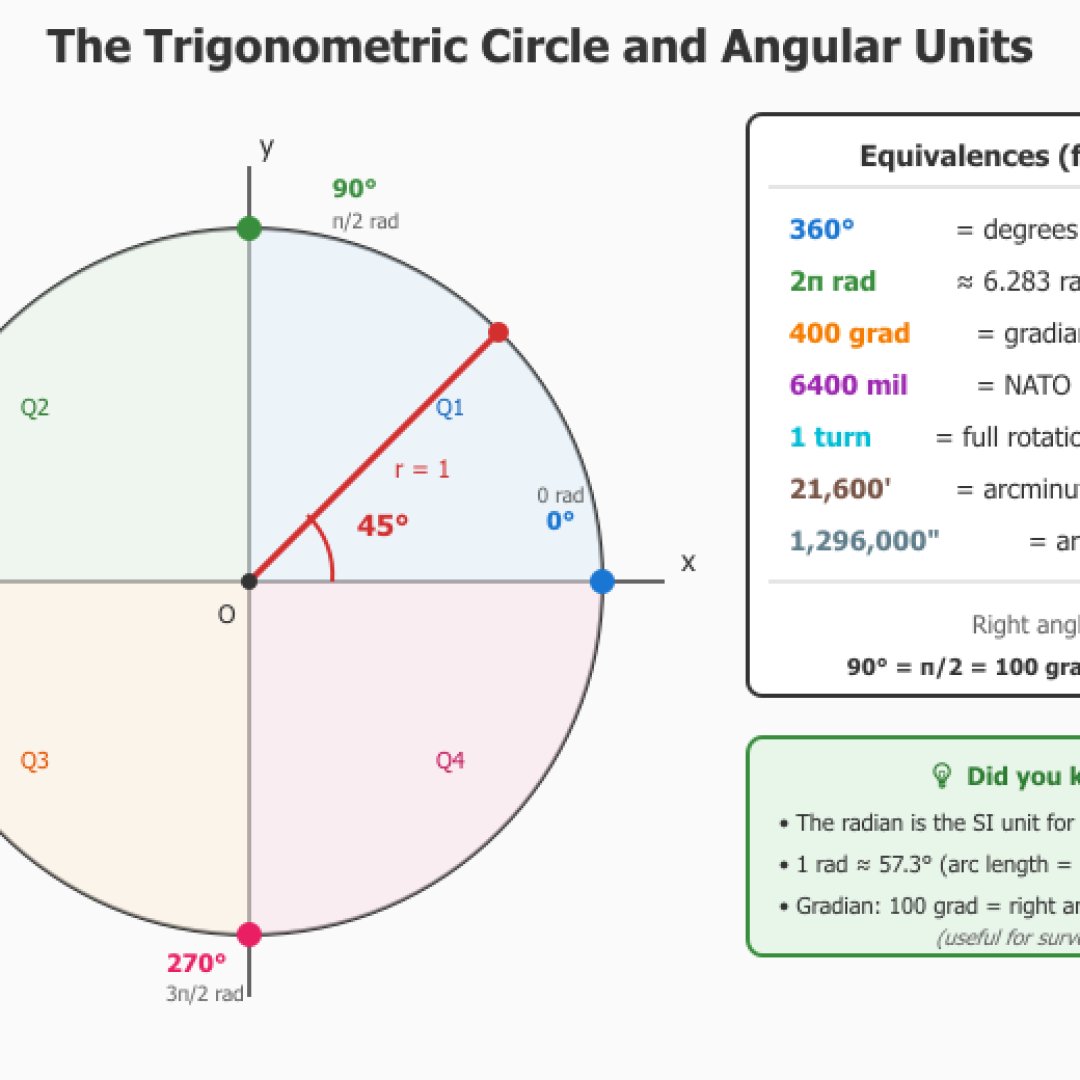
A visualização dinâmica mostrará o círculo trigonométrico assim como o triângulo de declive para compreender visualmente a relação que existe entre o ângulo e a inclinação. Os ângulos notáveis são detectados automaticamente (normalmente ^^) e exibem sua notação em π (por exemplo π/4 rad para 45°).
O cálculo de distância e ponto médio
Este módulo permite calcular a distância euclidiana entre dois pontos em duas dimensões ou em três dimensões. Quanto ao cálculo tridimensional, ele também determina o declive do terreno entre duas altitudes, o que pode ser útil em topografia assim como em caminhadas.
As fórmulas são baseadas no teorema de Pitágoras, demonstrado nos Elementos de Euclides (Livro I, Proposição 47):
- Distância 2D = √[(x₂-x₁)² + (y₂-y₁)²]
- Distância 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]
- Ponto médio = ((x₁+x₂)/2, (y₁+y₂)/2)
O módulo 3D também calcula os ângulos diretores do vetor deslocamento em relação aos três eixos X, Y e Z, o que pode ser útil em topografia e navegação mas na verdade é principalmente útil na escola!
Equação de reta (y = mx + b)
Permite gerar a equação de uma reta a partir de dois pontos ou de um declive e um ponto. Este módulo fornece três tipos de formas: a inclinação-ordenada (y = mx + b), o ponto-inclinação (y - y₁ = m(x - x₁)) assim como a forma padrão (Ax + By = C). Ele permite calcular a abscissa na origem, a ordenada na origem e verificar se três pontos são colineares com toda simplicidade.
A colinearidade será verificada pelo cálculo da área do triângulo formado pelos três pontos. Se a área for nula, os pontos estão então alinhados.
A visualização gráfica interativa
Usando um gráfico com a biblioteca Chart.js, permite traçar suas linhas e pontos. Você adiciona linhas por equação ou coordenadas. Você controla o zoom de ±5 a ±100. Você ativa e desativa as grades. E pode exportar o resultado seja em imagem PNG ou em formato vetorial SVG que permite não perder qualidade no aumento.
Linhas paralelas e perpendiculares
Permitem encontrar a equação de uma reta paralela ou perpendicular passando por um ponto dado. As regras matemáticas são as seguintes: duas linhas são paralelas se m₁ = m₂, perpendiculares se m₁ × m₂ = -1. O verificador integrado analisa a relação existente entre dois declives e calcula o ângulo formado entre duas retas secantes.
Essas propriedades decorrem diretamente da geometria euclidiana, noções fundamentais em geometria analítica para o estudo das retas no plano cartesiano.
Regressão linear
Permitirá calcular a linha de tendência pelo método dos mínimos quadrados inserindo seus dados manualmente, seja colando-os ou importando-os através de um arquivo CSV. O módulo calculará o coeficiente de correlação R, o coeficiente de determinação R² assim como o erro padrão e os resíduos. Assim, você pode fazer previsões de Y para X dado.
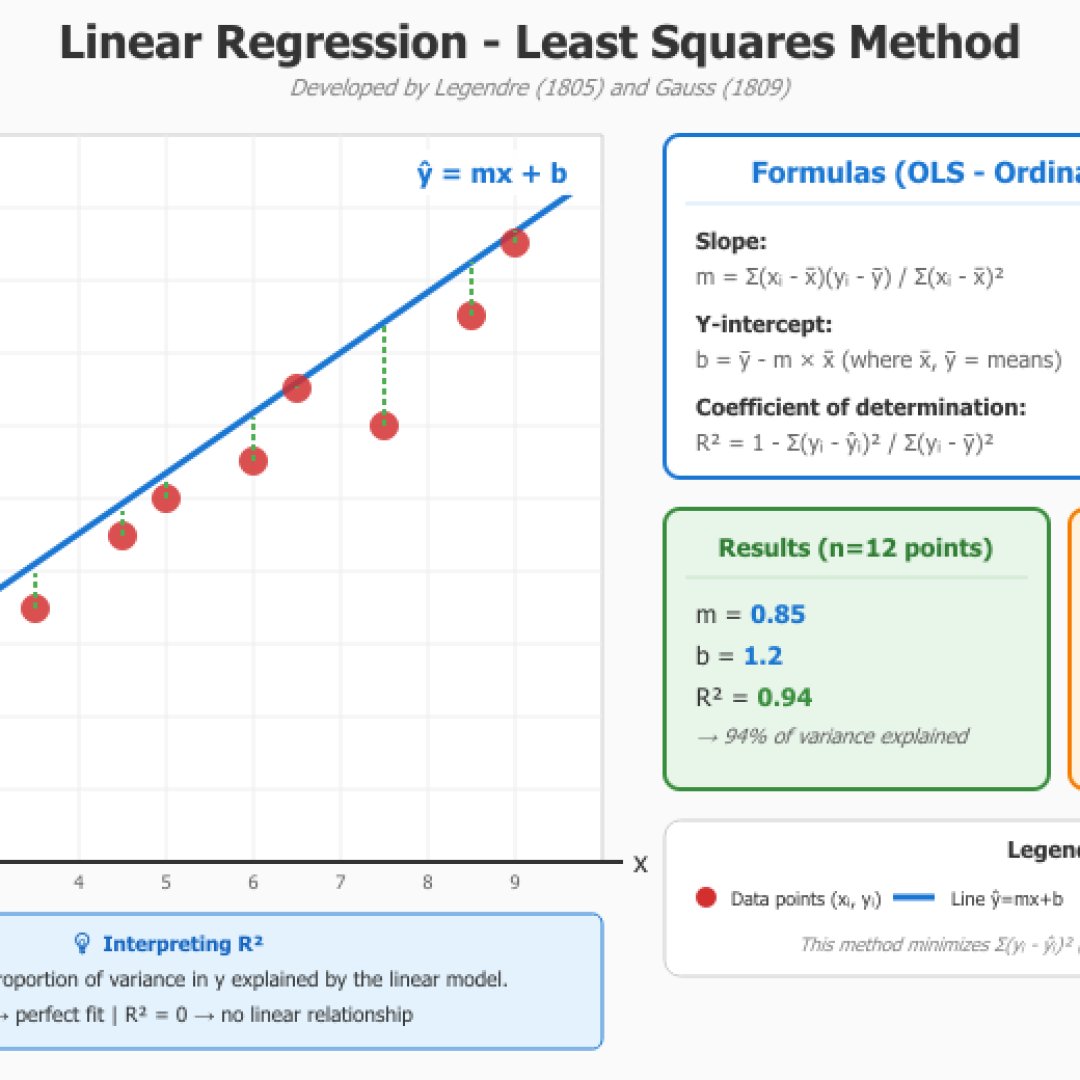
O método dos mínimos quadrados foi desenvolvido por Adrien-Marie Legendre (1805) e Carl Friedrich Gauss (1809), ele minimiza a soma dos quadrados dos desvios entre os valores observados e os valores previstos pelo modelo linear.
Ângulos e elevação
Você calcula os ângulos de elevação e depressão para seus projetos, seja por exemplo no âmbito do tiro balístico, do apontamento de seus telescópios para as estrelas, para calcular um ângulo de subida em avião ou o cálculo de um declive de rampa para suas atividades de construção. O cálculo inverso permite encontrar a distância ou a altura faltante a partir de um ângulo conhecido.
Este módulo aceita o ângulo de entrada nas 10 unidades suportadas, incluindo diretamente em porcentagem de declive.
Compreender simplesmente o cálculo de declive
O declive em porcentagem
A porcentagem de declive representará a relação que existe entre o desnível e a distância horizontal, tudo multiplicado por 100. Um declive de 10% significará então que para 100 metros de distância horizontal, você ganhará 10 metros de elevação. É o formato padrão que é usado nas placas rodoviárias e na construção.
O declive em grau
O ângulo do declive medirá a inclinação em relação à horizontal. Assim, um ângulo de 45 graus corresponde a um declive de 100% (altura igual distância). A conversão usa a função tangente: % = tan(ângulo) × 100.
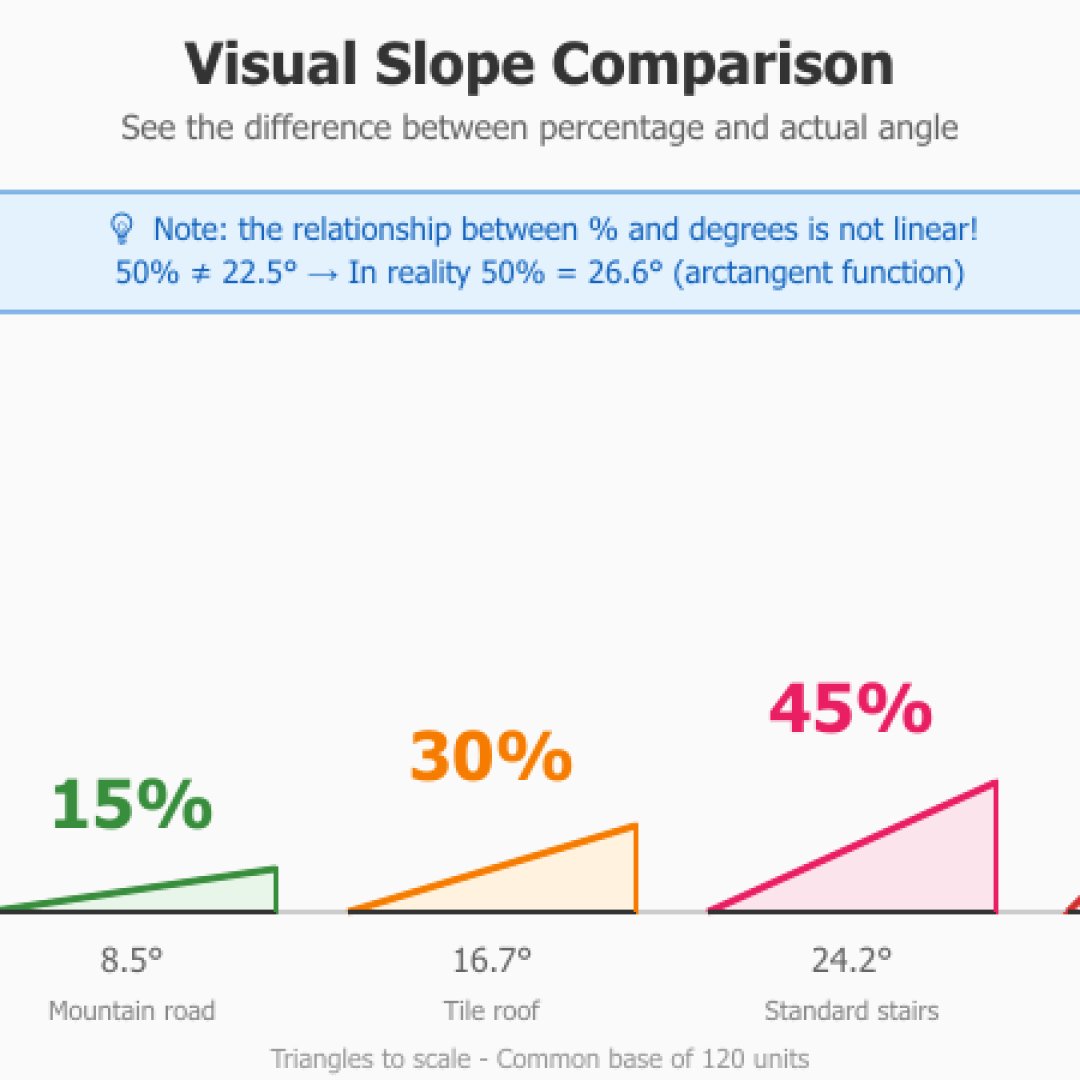
Correspondências comuns
| Porcentagem | Ângulo | Uso típico |
|---|---|---|
| 5% | 2.9° | Rampa PMR (máximo legal) |
| 10% | 5.7° | Ciclovia, alameda |
| 15% | 8.5° | Estrada de montanha |
| 30% | 16.7° | Escada suave, telhado baixo declive |
| 45% | 24.2° | Escada padrão |
| 100% | 45° | Declive máximo praticável |
Aplicações práticas
Cálculo de declive de telhado
O declive do teto influencia necessariamente a escolha dos materiais de cobertura assim como o escoamento das águas pluviais. Os telhados terraço necessitam em geral um 5% mínimo para assegurar a evacuação das águas pluviais. Os tetos de telhas pedem geralmente 15 a 35% segundo o tipo de telha (telhas mecânicas, telhas canal ou ardósias). As zonas de montanha com neve requerem declives mais fortes de 35% a 60% para evitar que os tetos desabem no inverno sob o peso da neve.
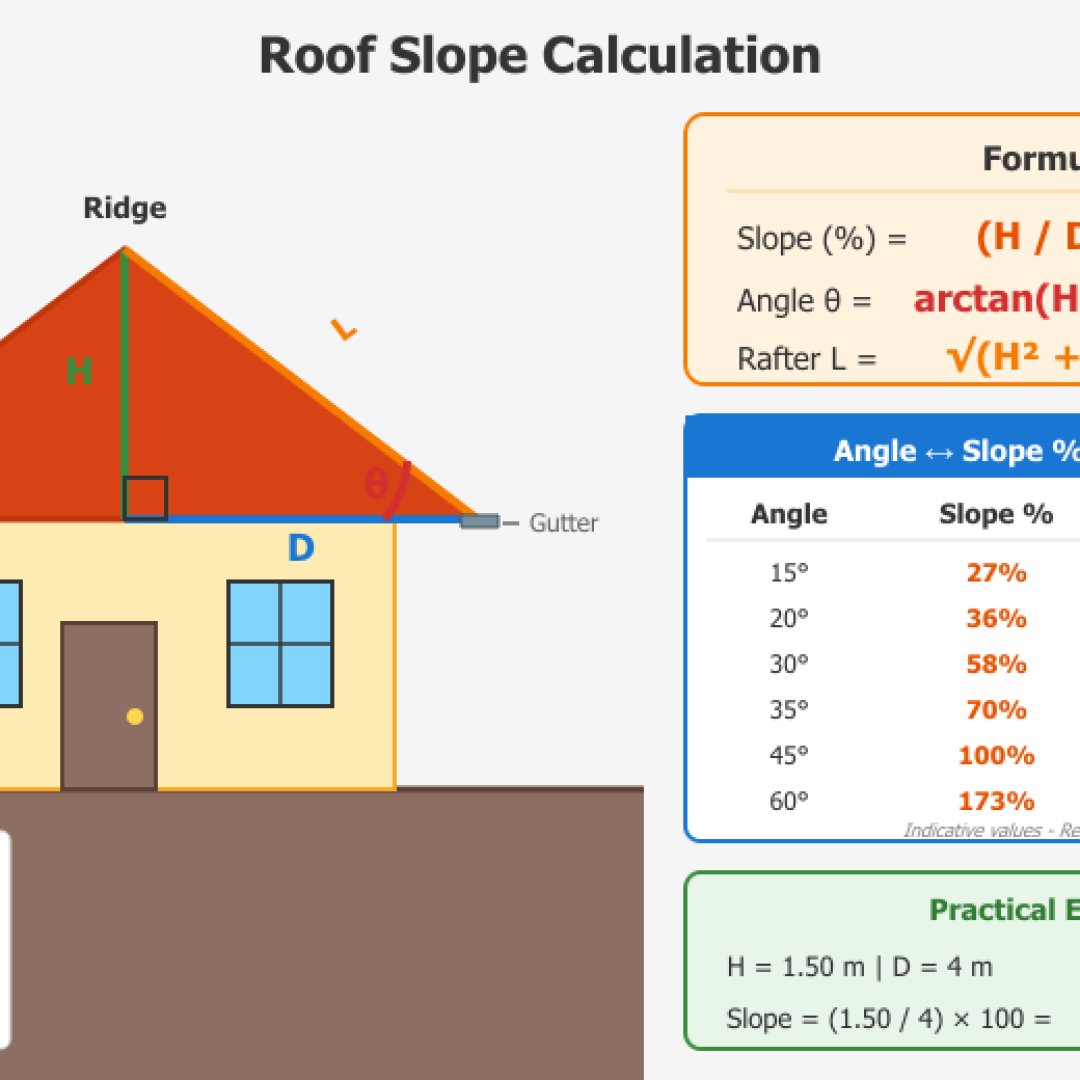
Assim, para calcular o declive do seu teto, você deve medir a altura do frontão e a distância horizontal (a meia largura do edifício para um teto de duas águas). Nossa pequena calculadora de declive de telhado dá o resultado em porcentagem e em grau.
A rampa para pessoas com mobilidade reduzida (PMR) e acessibilidade
A regulamentação francesa impõe um declive máximo de 5% para as rampas de acesso PMR (pessoas com mobilidade reduzida). No entanto, derrogações permitem até 8% em 2 metros no máximo ou 10% em 50 cm. Nossa calculadora permitirá verificar a conformidade do seu projeto de melhoria da acessibilidade PMR.
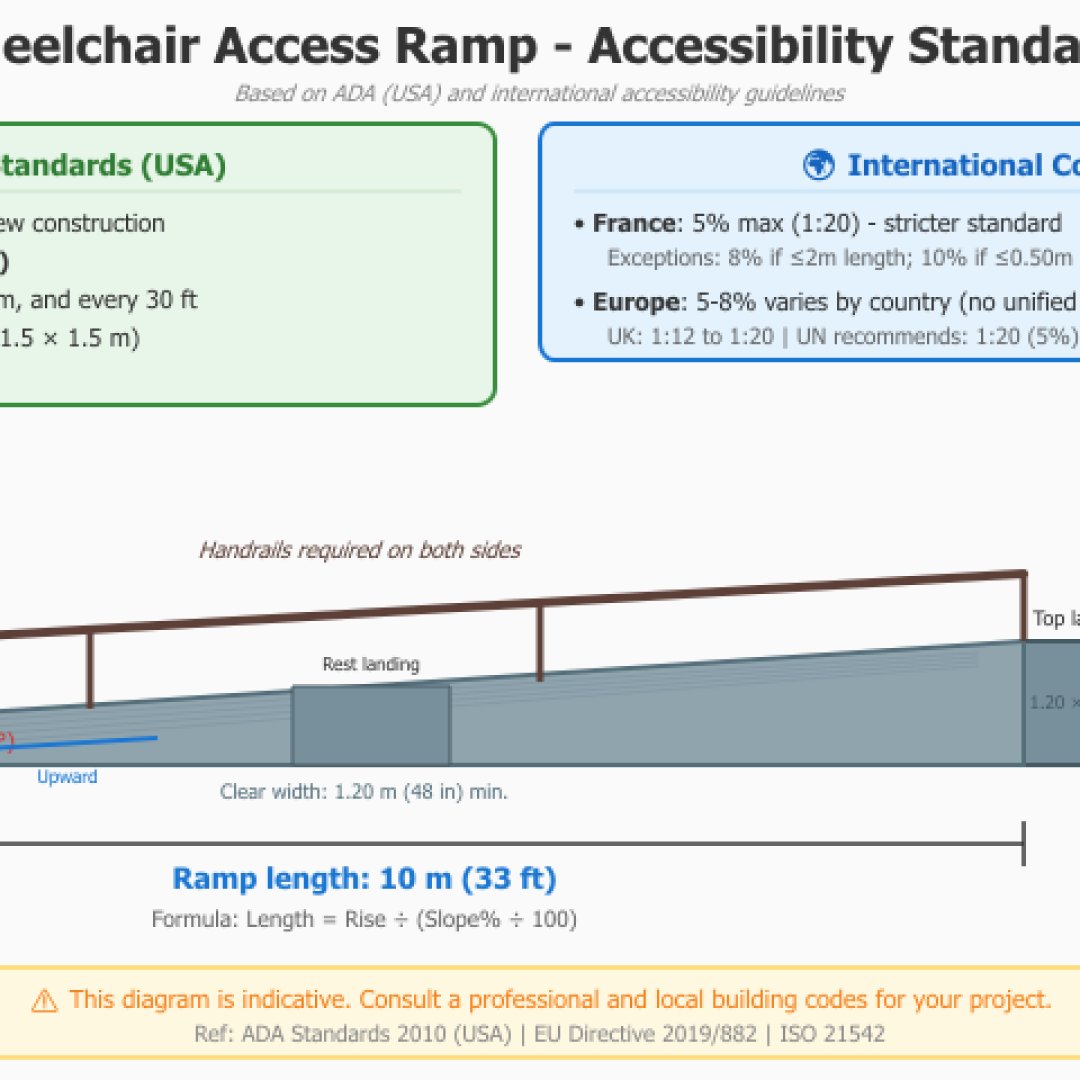
Referência: Decreto de 20 de abril de 2017 relativo à acessibilidade às pessoas com deficiência dos estabelecimentos que recebem o público.
A título de comparação, a regulamentação americana ADA (Americans with Disabilities Act) também impõe uma razão máxima de 1:12 (seja 8.33%) para as rampas de acesso público.
Topografia e terreno
É preciso saber que em topografia, o declive será calculado entre dois pontos de medida a diferentes altitudes. As curvas de nível nos mapas IGN permitem determinar o desnível (a equidistância é igual à diferença de altitude entre duas curvas de nível). Nosso pequeno módulo calculará o declive real do terreno levando em conta a altitude.
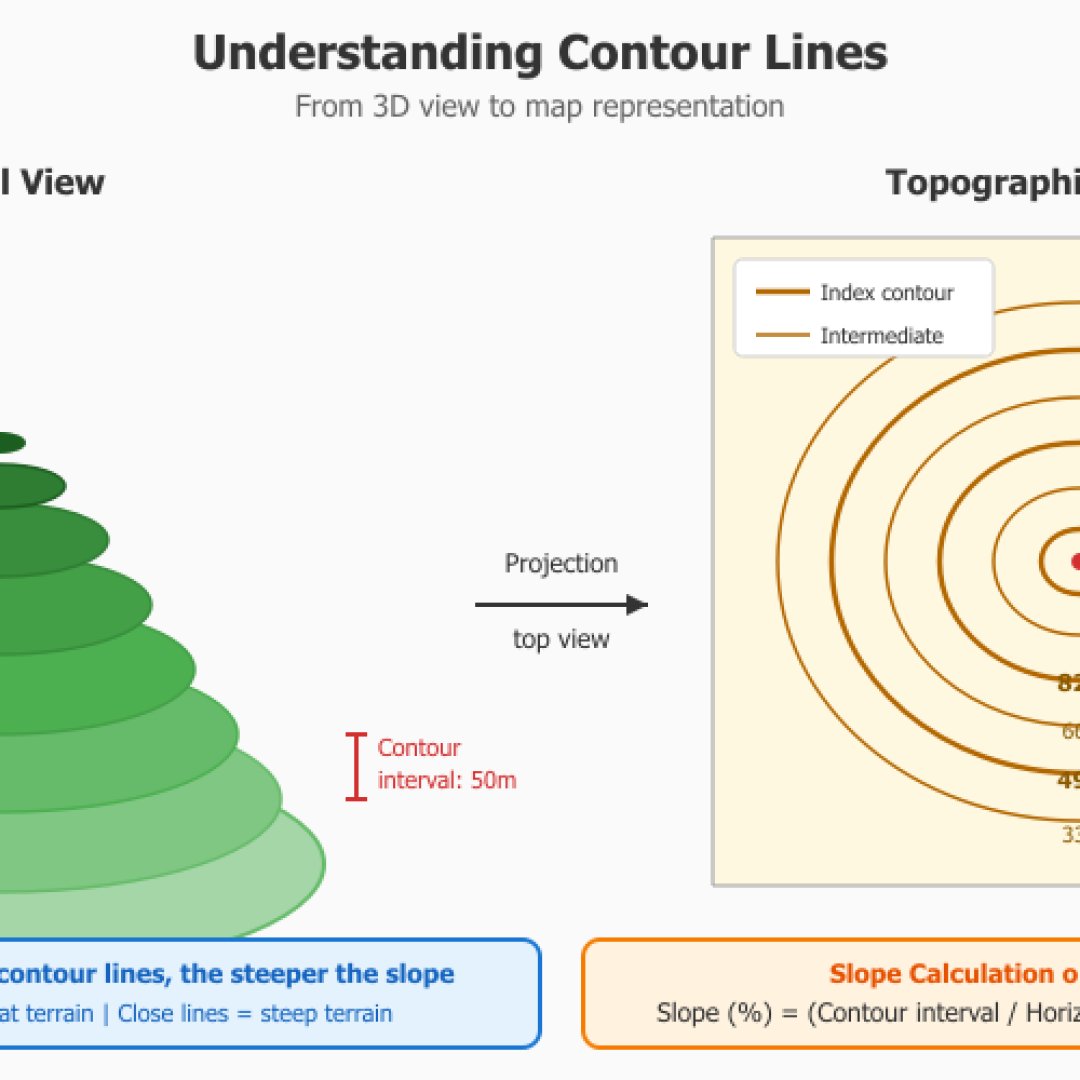
Em topografia profissional, a unidade gradiano (ou gon) é frequentemente preferida pois divide o círculo em 400 partes, o que simplifica os cálculos (um ângulo reto = 100 grad exatamente), por outro lado no âmbito militar se expressa frequentemente em milésimo no exército terrestre e mais em graus ao nível OTAN.
Estrutura e construção
O cálculo da sua estrutura de madeira dependerá do declive escolhido. Um telhado constituído de uma ou duas águas necessita caibros que serão dimensionados segundo a inclinação e o vão. O comprimento do declive (que corresponde à hipotenusa) determinará a quantidade de materiais de cobertura necessários para seu projeto.
Fórmulas de referência
Cálculo da porcentagem de declive
Declive (%) = (Altura / Distância horizontal) × 100Conversão porcentagem para graus
Ângulo (°) = arctan(Declive% / 100) × (180 / π)Conversão graus para radianos
Radianos = Graus × (π / 180)Comprimento do declive (teorema de Pitágoras)
Comprimento = √(Altura² + Distância²)Relações trigonométricas
tan(ângulo) = Altura / Distância = Declive% / 100
sin(ângulo) = Altura / Hipotenusa
cos(ângulo) = Distância / HipotenusaConversões de unidades angulares
Gradianos = Graus × (400 / 360)
Mils NATO = Graus × (6400 / 360)
Minutos de arco = Graus × 60
Segundos de arco = Graus × 3600
Voltas = Graus / 360
Milirradianos = Radianos × 1000Equação de reta
Forma inclinação-ordenada : y = mx + b
Forma ponto-inclinação : y - y₁ = m(x - x₁)
Forma padrão : Ax + By = CRegressão linear (método dos mínimos quadrados)
Declive (m) = [n∑xy - ∑x∑y] / [n∑x² - (∑x)²]
Ordenada (b) = ȳ - m × x̄
Coeficiente R² = 1 - [∑(y - ŷ)² / ∑(y - ȳ)²]Distância euclidiana
Distance 2D = √[(x₂-x₁)² + (y₂-y₁)²]
Distance 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]Linhas paralelas e perpendiculares
Paralelas : m₁ = m₂
Perpendiculares : m₁ × m₂ = -1Unidades angulares: guia de referência
| Unidade | Símbolo | Círculo completo | Uso principal |
|---|---|---|---|
| Grau | ° | 360° | Geometria, construção, navegação |
| Radiano | rad | 2π ≈ 6.283 | Matemática, física, engenharia |
| Gradiano | grad | 400 grad | Topografia, geodésia (Europa) |
| Volta | turn | 1 turn | Programação (CSS), robótica |
| Milirradiano | mrad | ~6283 mrad | Balística, óptica, lunetas de tiro |
| Mil NATO | mil | 6400 mil | Aplicações militares OTAN |
| Minuto de arco | ′ | 21 600′ | Astronomia, navegação marítima |
| Segundo de arco | ″ | 1 296 000″ | Alta precisão, coordenadas GPS |
O radiano é a unidade de ângulo do Sistema Internacional (SI), definido pelo BIPM na Brochura SI. Ele corresponde ao ângulo no centro que intercepta um arco de comprimento igual ao raio do círculo (Imagine um círculo: é o ângulo no centro que corta um arco (uma porção da circunferência) exatamente do mesmo comprimento que o raio do círculo. É como se você desenrolasse o raio ao longo da borda do círculo para formar esse ângulo base!).
Perguntas frequentes
Como calcular um declive em porcentagem?
Você simplesmente divide a altura (desnível) pela distância horizontal. Depois multiplica tudo por 100. Por exemplo, 5 metros de desnível em 50 metros de distância corresponderá a 10% de declive. Nossa ferramenta permite fazer esse cálculo automaticamente.
Qual é a diferença entre uma porcentagem e os graus?
De um lado a porcentagem representará uma razão que corresponde à altura dividida pela distância multiplicada por 100, e os graus medirão o ângulo geométrico. A relação não é linear. Ou seja, 100% é igual a 45 graus. Mas 50% não será 22,5 graus. Na realidade são 26,6 graus. Esta não-linearidade provém da função arctangente (perfeito para brilhar em sociedade) usada para a conversão.
Como calcular o declive de um teto?
Você deve medir a altura da cumeeira desde o nível das calhas e a distância horizontal até o ponto de medida. Em seguida, use nossa calculadora de declive de telhado para obter a porcentagem e verificar a compatibilidade com seu revestimento, sejam telhas, ardósias ou chapas.
Qual declive para um telhado de chapa de aço?
A chapa de aço aceita declives menores, geralmente a partir de 5% (3 graus), segundo as recomendações DTU. Os declives inferiores necessitam uma impermeabilização reforçada para seu projeto.
Referência: NF DTU 40.35 - Cobertura em placas nervuradas oriundas de chapas de aço revestidas (AFNOR).
Como medir um declive no terreno?
Muito simplesmente. Se você está equipado, use um nível laser rotativo, um clinômetro ou um aplicativo de smartphone com acelerômetro. E para grandes distâncias, você registra a altitude em dois pontos, seja com um sistema GPS que permite fazer um levantamento altimétrico, ou simplesmente você calcula a partir da sua posição desde um mapa topográfico. E você mede a distância horizontal percorrida.
O que é o coeficiente R² em regressão linear?
O coeficiente de determinação R² indica a proporção da variância dos dados que é explicada pelo modelo linear. Um R² de 0.95 significa que 95% da variação dos dados é explicada pela reta de regressão. Quanto mais R² está próximo de 1, melhor é o ajuste do modelo.
Por que usar nossa calculadora?
Nossa suíte de cálculos de declive oferece 8 módulos complementares, que cobrem o máximo das necessidades existentes, seja do simples cálculo de porcentagem até a regressão linear avançada que dá dor de cabeça. A interface permite realizar seus cálculos simplesmente desde seu telefone celular, seu tablet ou seu computador. Saiba que todos os cálculos se efetuam desde seu navegador, para máxima rapidez e garantir uma confidencialidade total dos dados que você submete.
Tentamos colocar o máximo de unidades angulares disponíveis para todos, no mesmo lugar (graus, radianos, gradianos, porcentagens, razões, milirradianos, mils NATO, minutos e segundos de arco e as voltas). Normalmente, eles respondem às necessidades dos profissionais da construção, da topografia, balística, astronomia e dos alunos estudiosos.
Calcule seu declive agora com nossas ferramentas gratuitas.