Online Neigungsrechner - Unsere 8 kostenlosen Tools
Unsere umfassende Suite von Neigungsberechnungen ermöglicht es Ihnen, eine Neigung zu berechnen, sei es in Prozent, in Grad, in Radiant, aber auch in allen existierenden Winkel- und Neigungseinheiten. Ob Sie die Neigung Ihres Daches, einer Rampe für barrierefreien Zugang, Ihres Geländes oder einer bestimmten Straße berechnen müssen, unsere Tools decken ein breites Spektrum von Anwendungsfällen ab. Keine Registrierung erforderlich, die Berechnung erfolgt 100% clientseitig, also in Ihrem Browser, Ihre Daten bleiben privat.
Unsere 8 Berechnungsmodule
Der grundlegende Neigungsrechner
Er ermöglicht die Berechnung der Neigung aus Höhe und horizontaler Entfernung oder direkt aus einem Winkel, falls Sie ihn kennen. Sie geben Ihr Gefälle und die zurückgelegte Entfernung ein, um den Neigungsprozentsatz sowie den Winkel in Grad, in Radiant, das Verhältnis und die Hypotenusenlänge zu erhalten.
Die verwendete Formel ist relativ einfach, es handelt sich um die Neigung in Prozent, die gleich der Höhe geteilt durch die horizontale Entfernung multipliziert mit 100 ist: Neigung (%) = (Höhe / Horizontale Entfernung) × 100. Bezüglich des Winkels θ: θ = arctan(Höhe / Entfernung). Der Rechner kategorisiert automatisch die Neigung, er klassifiziert sie von sehr sanft bis extrem mit Beispielen konkreter Anwendungen.
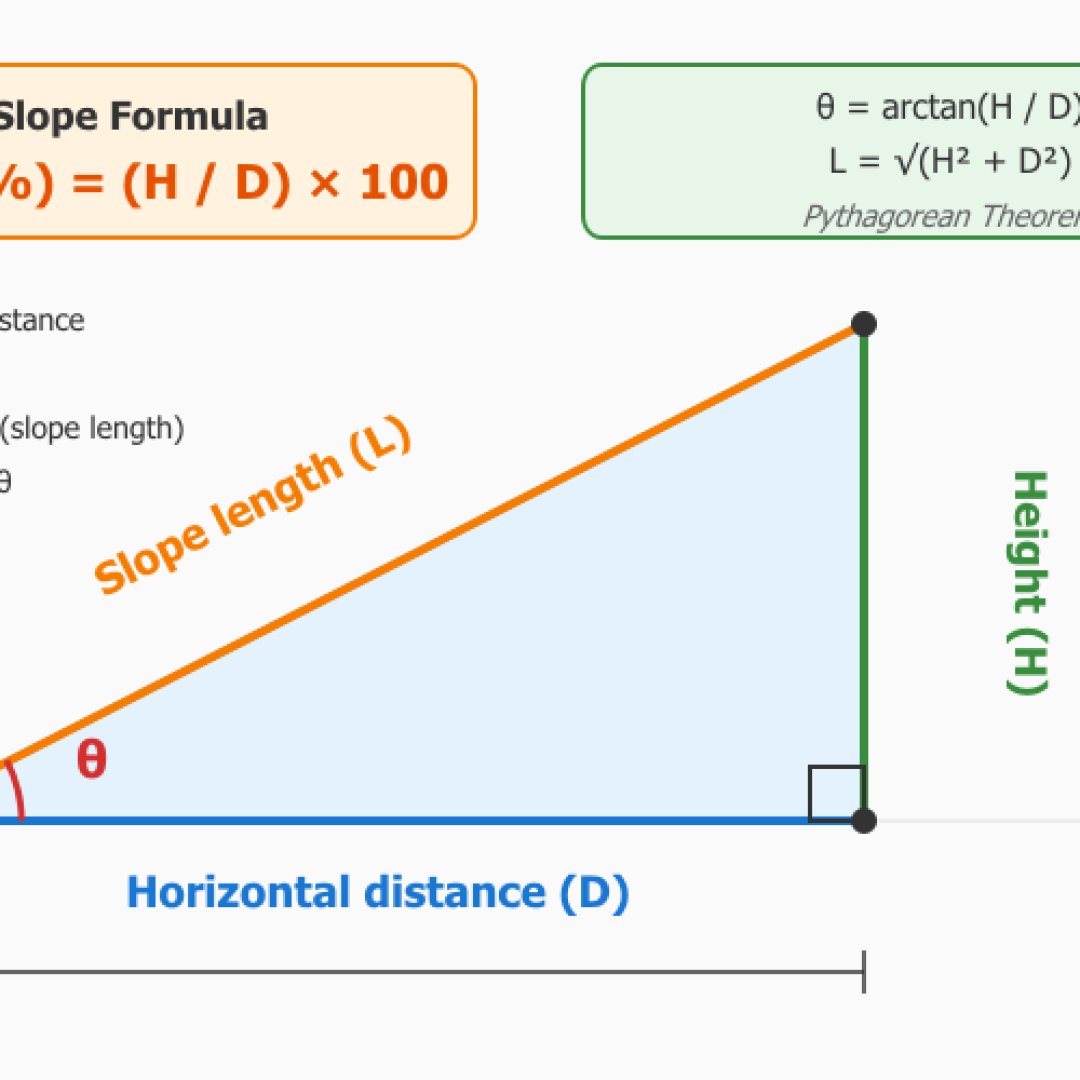
Dieses Modul ermöglicht es Ihnen auch, die umgekehrte Berechnung durchzuführen. Das heißt, ausgehend von einem bekannten Winkel und einer Dimension (horizontale Entfernung, Höhe oder Hypotenuse) bestimmt es die beiden anderen fehlenden Dimensionen dank der grundlegenden trigonometrischen Beziehungen.
Der Winkeleinheiten-Konverter
Der Winkeleinheiten-Konverter ist vollständig und ermöglicht es Ihnen, direkt von einer Einheit zur anderen zu wechseln. Er unterstützt 10 Arten von Einheiten, sei es Prozent, Grad, Radiant, Gon (in der Topographie verwendet), Umdrehungen (zum Beispiel in CSS verwendet), Milliradiant (Ballistik), NATO-Mil (militärisch), Bogenminuten und Bogensekunden (Astronomie) und das Verhältnis (1:X).
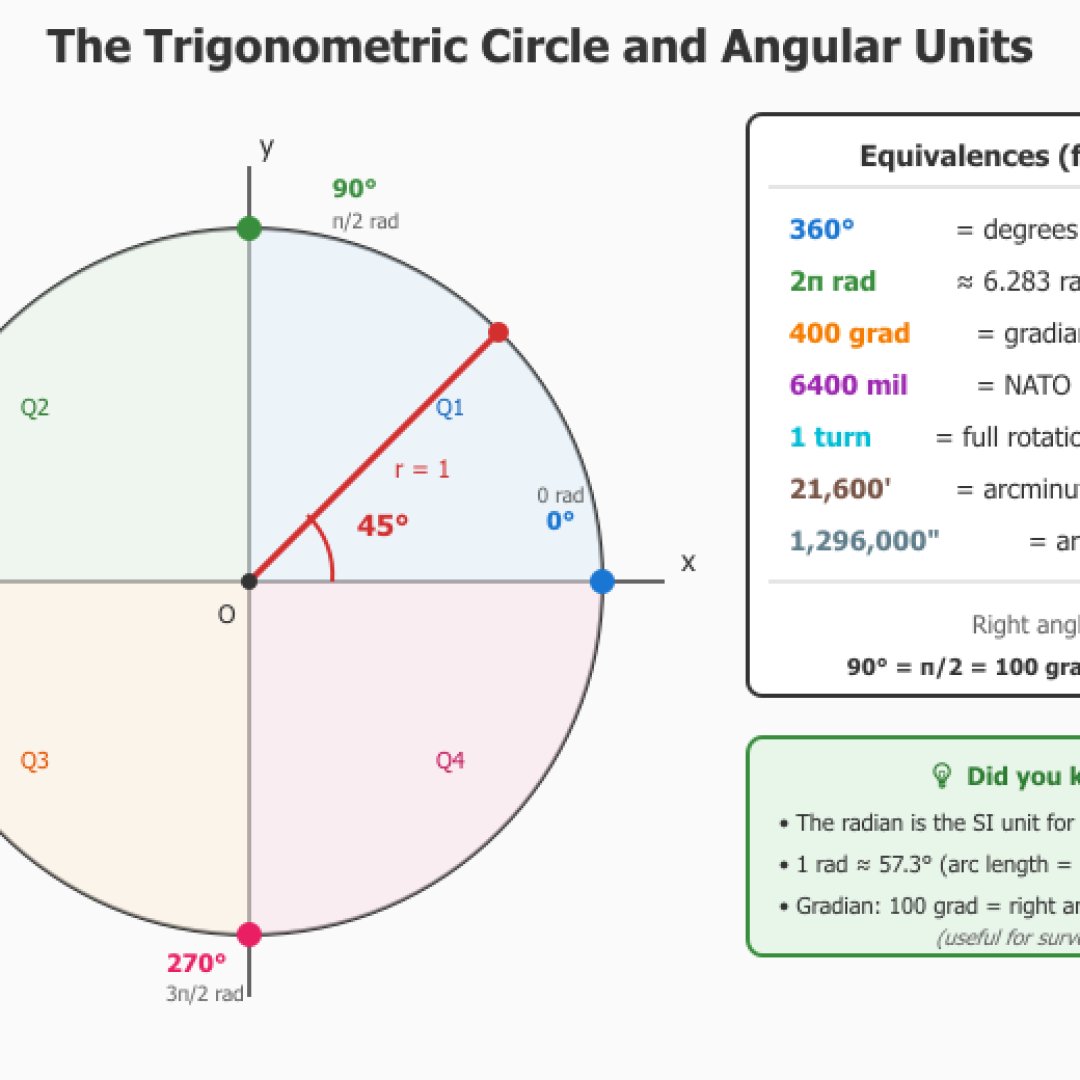
Die dynamische Visualisierung zeigt Ihnen den trigonometrischen Kreis sowie das Neigungsdreieck, um die Beziehung zwischen Winkel und Neigung visuell zu verstehen. Bemerkenswerte Winkel werden automatisch erkannt (normalerweise ^^) und zeigen ihre Notation in π (zum Beispiel π/4 rad für 45°).
Die Entfernungs- und Mittelpunktberechnung
Dieses Modul ermöglicht die Berechnung der euklidischen Entfernung zwischen zwei Punkten in zwei oder drei Dimensionen. Bei der dreidimensionalen Berechnung bestimmt es auch die Geländeneigung zwischen zwei Höhen, was in der Topographie sowie beim Wandern nützlich sein kann.
Die Formeln basieren auf dem Satz des Pythagoras, bewiesen in Euklids Elementen (Buch I, Satz 47):
- Entfernung 2D = √[(x₂-x₁)² + (y₂-y₁)²]
- Entfernung 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]
- Mittelpunkt = ((x₁+x₂)/2, (y₁+y₂)/2)
Das 3D-Modul berechnet auch die Richtungswinkel des Verschiebungsvektors bezüglich der drei Achsen X, Y und Z, was in der Topographie und Navigation nützlich sein kann, aber ehrlich gesagt ist es hauptsächlich in der Schule nützlich!
Geradengleichung (y = mx + b)
Ermöglicht die Generierung einer Geradengleichung aus zwei Punkten oder einer Neigung und einem Punkt. Dieses Modul bietet drei Arten von Formen: die Steigung-Achsenabschnitt-Form (y = mx + b), die Punkt-Steigung-Form (y - y₁ = m(x - x₁)) sowie die Standardform (Ax + By = C). Es ermöglicht Ihnen, den x-Achsenabschnitt, den y-Achsenabschnitt zu berechnen und zu überprüfen, ob drei Punkte kollinear sind, ganz einfach.
Die Kollinearität wird durch die Berechnung der Fläche des von den drei Punkten gebildeten Dreiecks überprüft. Wenn die Fläche null ist, sind die Punkte dann ausgerichtet.
Die interaktive grafische Visualisierung
Mit einem Diagramm unter Verwendung der Chart.js-Bibliothek ermöglicht es das Zeichnen Ihrer Linien und Punkte. Sie fügen Linien per Gleichung oder Koordinaten hinzu. Sie kontrollieren den Zoom von ±5 bis ±100. Sie aktivieren und deaktivieren die Gitter. Und Sie können das Ergebnis entweder als PNG-Bild oder im Vektorformat SVG exportieren, das beim Vergrößern keinen Qualitätsverlust aufweist.
Parallele und senkrechte Linien
Ermöglichen es Ihnen, die Gleichung einer parallelen oder senkrechten Geraden zu finden, die durch einen gegebenen Punkt verläuft. Die mathematischen Regeln sind folgende: zwei Linien sind parallel, wenn m₁ = m₂, senkrecht, wenn m₁ × m₂ = -1. Der integrierte Prüfer analysiert die bestehende Beziehung zwischen zwei Steigungen und berechnet den Winkel zwischen zwei sich schneidenden Geraden.
Diese Eigenschaften ergeben sich direkt aus der euklidischen Geometrie, grundlegende Begriffe in der analytischen Geometrie für das Studium von Geraden in der kartesischen Ebene.
Lineare Regression
Ermöglicht es Ihnen, die Trendlinie mit der Methode der kleinsten Quadrate zu berechnen, indem Sie Ihre Daten manuell eingeben, sie einfügen oder über eine CSV-Datei importieren. Das Modul berechnet den Korrelationskoeffizienten R, den Bestimmtheitskoeffizienten R² sowie den Standardfehler und die Residuen. So können Sie Vorhersagen von Y für gegebenes X treffen.
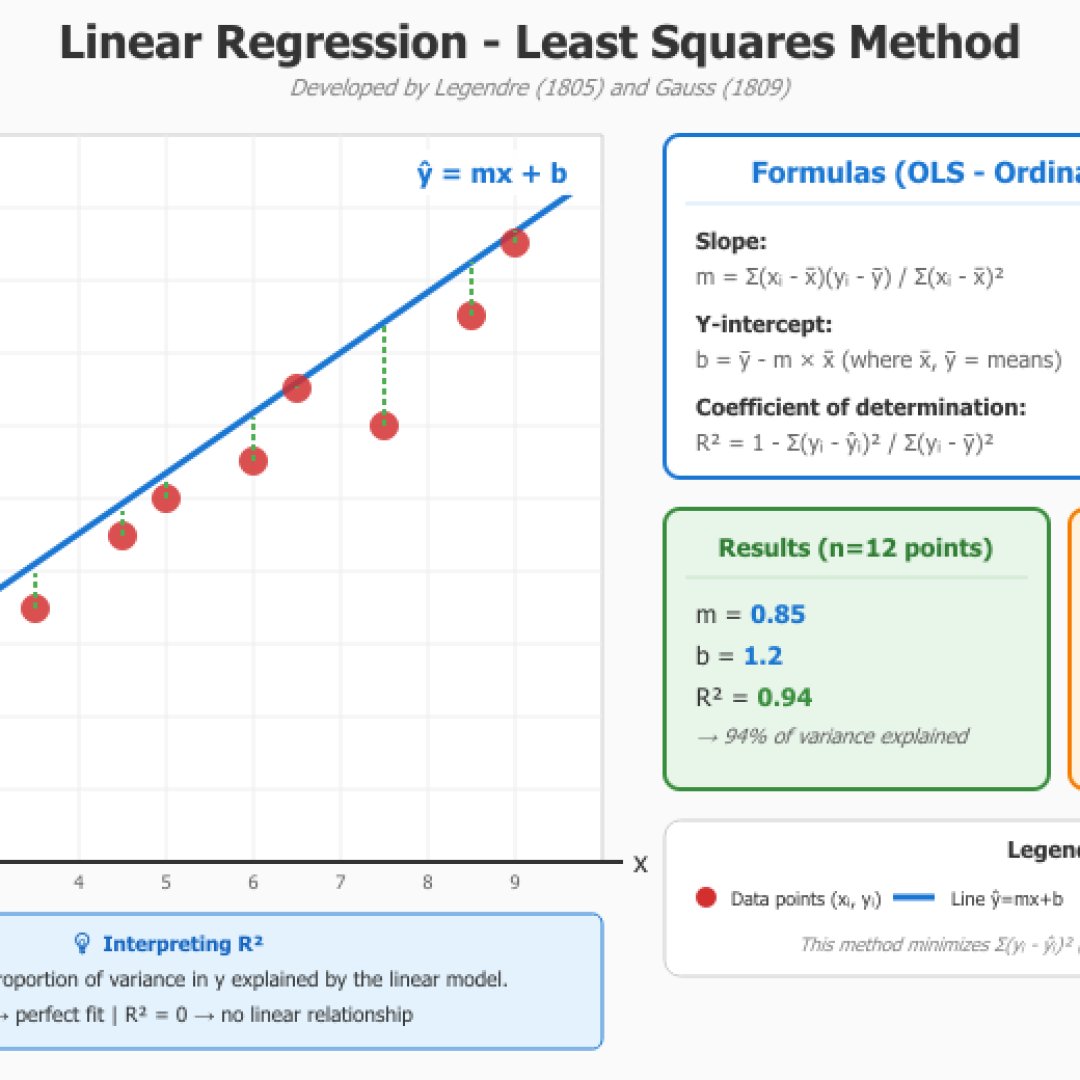
Die Methode der kleinsten Quadrate wurde von Adrien-Marie Legendre (1805) und Carl Friedrich Gauss (1809) entwickelt, sie minimiert die Summe der Quadrate der Abweichungen zwischen den beobachteten Werten und den vom linearen Modell vorhergesagten Werten.
Winkel und Elevation
Sie berechnen Elevations- und Depressionswinkel für Ihre Projekte, sei es zum Beispiel im Rahmen des ballistischen Schießens, der Ausrichtung Ihrer Teleskope auf die Sterne, zur Berechnung eines Steigwinkels im Flugzeug oder der Berechnung einer Rampenneigung für Ihre Bauaktivitäten. Die umgekehrte Berechnung ermöglicht es, die fehlende Entfernung oder Höhe aus einem bekannten Winkel zu finden.
Dieses Modul akzeptiert den Eingabewinkel in den 10 unterstützten Einheiten, einschließlich direkt als Neigungsprozentsatz.
Neigungsberechnung einfach verstehen
Die Neigung in Prozent
Der Neigungsprozentsatz stellt das Verhältnis zwischen dem Gefälle und der horizontalen Entfernung dar, das Ganze multipliziert mit 100. Eine Neigung von 10% bedeutet dann, dass Sie für 100 Meter horizontale Entfernung 10 Meter Höhengewinn haben. Dies ist das Standardformat, das auf Straßenschildern und im Bauwesen verwendet wird.
Die Neigung in Grad
Der Neigungswinkel misst die Neigung bezüglich der Horizontalen. So entspricht ein Winkel von 45 Grad einer Neigung von 100% (Höhe gleich Entfernung). Die Umrechnung verwendet die Tangensfunktion: % = tan(Winkel) × 100.
Häufige Entsprechungen
| Prozentsatz | Winkel | Typische Verwendung |
|---|---|---|
| 5% | 2,9° | Behindertenrampe (gesetzliches Maximum) |
| 10% | 5,7° | Radweg, Allee |
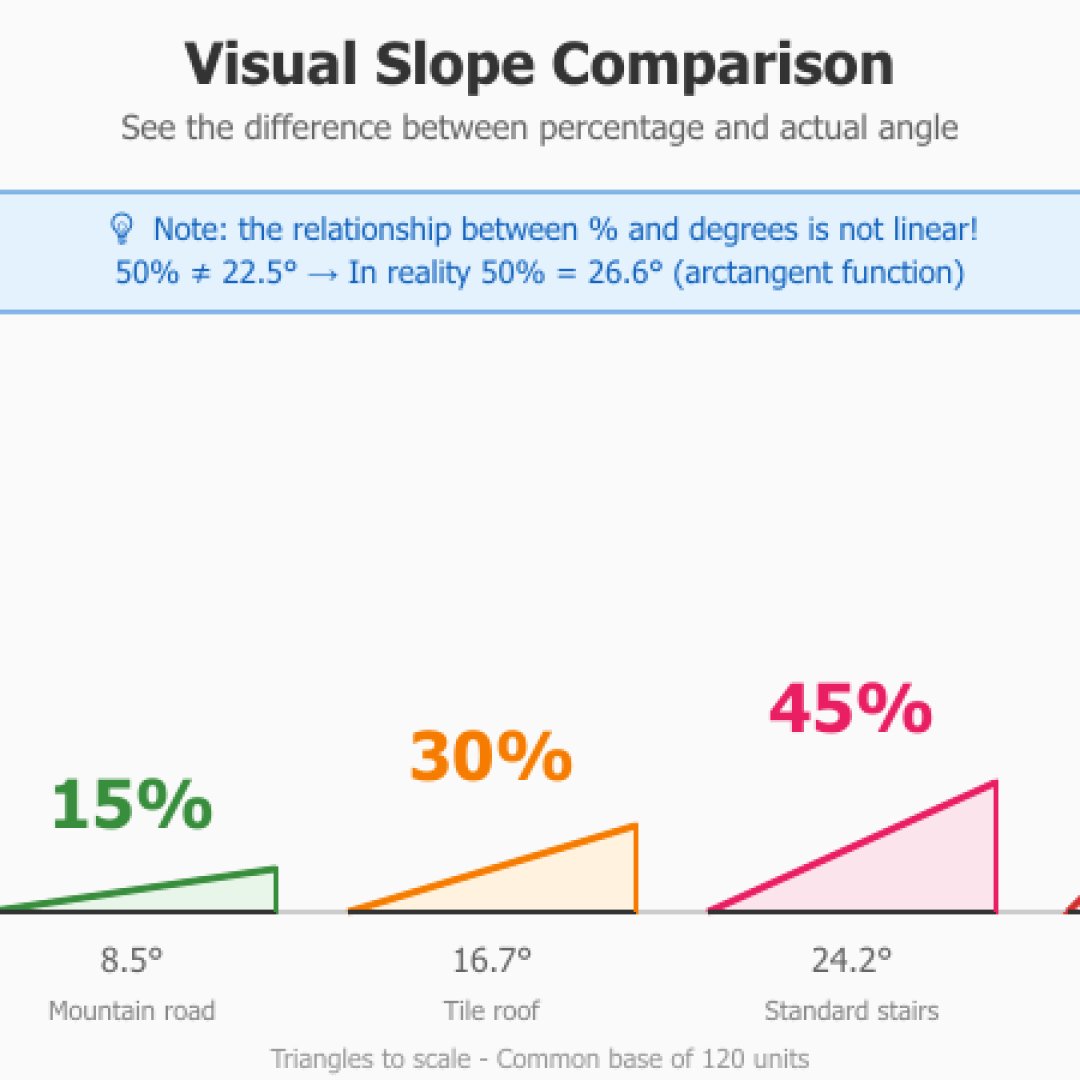
| 15% | 8,5° | Bergstraße |
| 30% | 16,7° | Sanfte Treppe, flach geneigtes Dach |
| 45% | 24,2° | Standard-Treppe |
| 100% | 45° | Maximal begehbare Neigung |
Praktische Anwendungen
Dachneigungsberechnung
Die Dachneigung beeinflusst notwendigerweise die Wahl der Deckungsmaterialien sowie den Regenwasserabfluss. Flachdächer benötigen im Allgemeinen mindestens 5%, um die Regenwasserentwässerung zu gewährleisten. Ziegeldächer erfordern normalerweise 15 bis 35% je nach Ziegeltyp (Betondachsteine, Hohlziegel oder Schiefer). Verschneite Berggebiete erfordern steilere Neigungen von 35% bis 60%, um zu verhindern, dass die Dächer im Winter unter dem Gewicht des Schnees einstürzen.
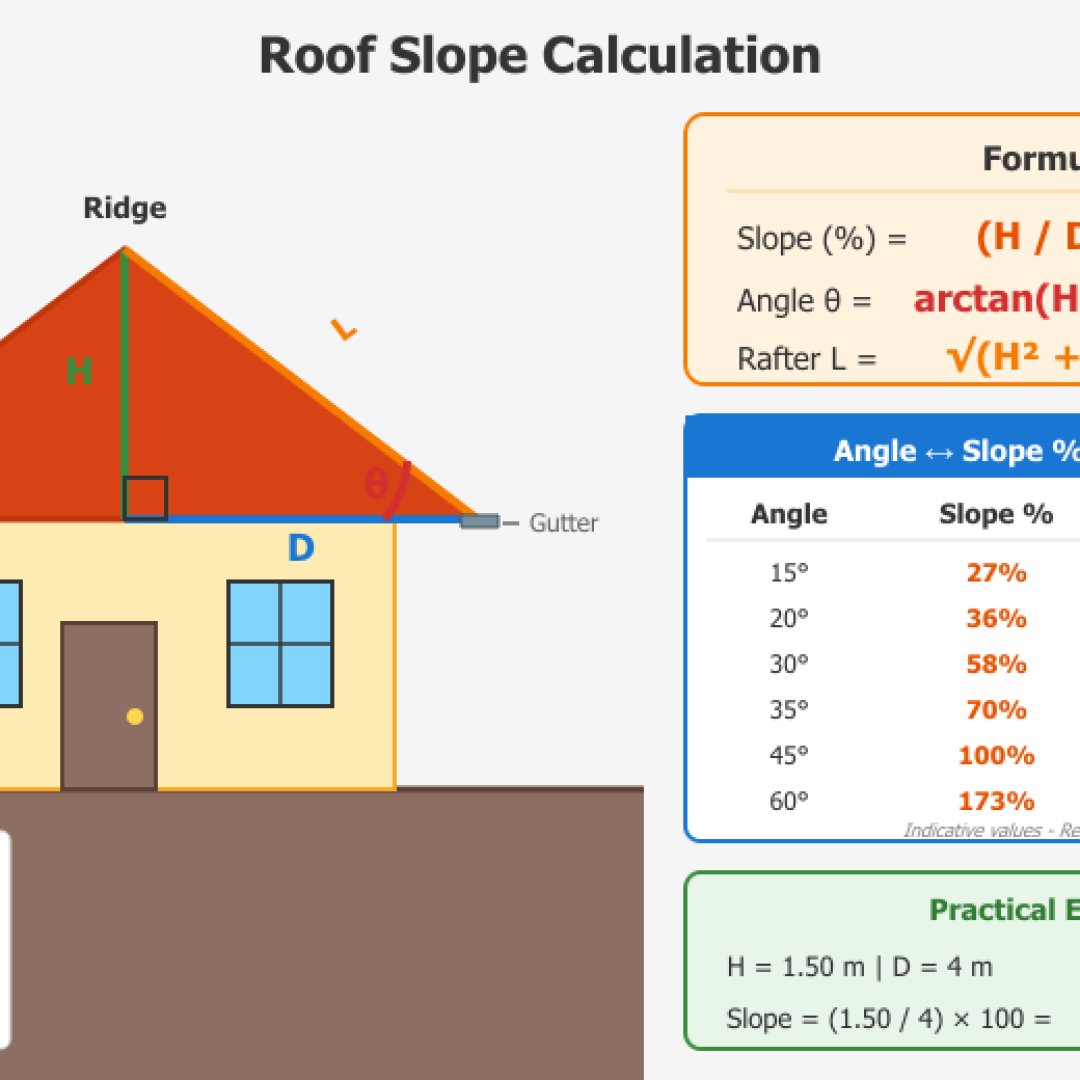
Um die Neigung Ihres Daches zu berechnen, müssen Sie die Höhe des Giebels und die horizontale Entfernung (die halbe Breite des Gebäudes für ein Satteldach) messen. Unser kleiner Dachneigungsrechner gibt das Ergebnis in Prozent und Grad an.
Die Rampe für Personen mit eingeschränkter Mobilität und Barrierefreiheit
Die französische Verordnung schreibt eine maximale Neigung von 5% für Zugangsrampen für Personen mit eingeschränkter Mobilität vor. Jedoch erlauben Ausnahmegenehmigungen bis zu 8% auf maximal 2 Metern oder 10% auf 50 cm. Unser Rechner ermöglicht es, die Konformität Ihres Barrierefreiheitsprojekts zu überprüfen.
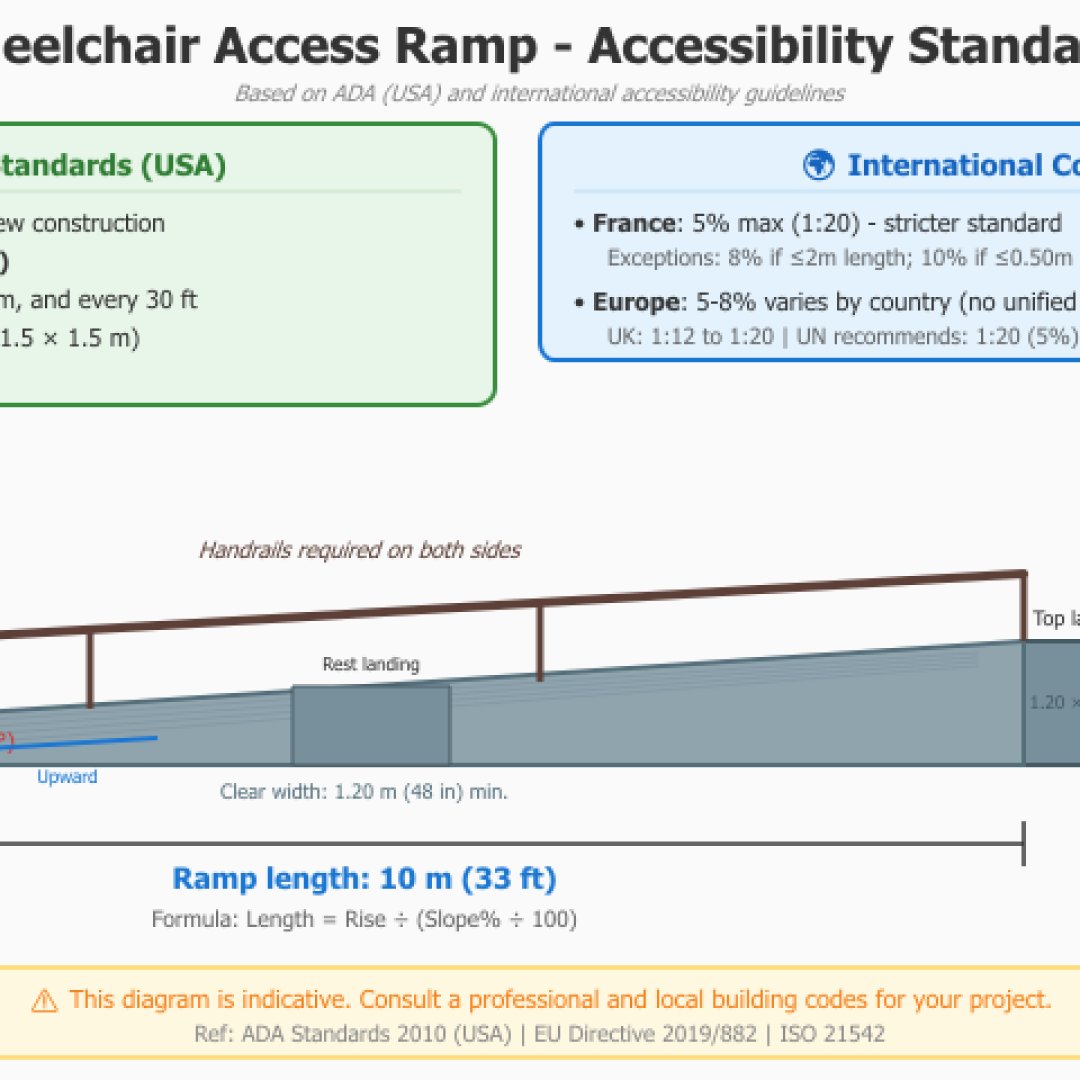
Referenz: Verordnung vom 20. April 2017 zur Barrierefreiheit für behinderte Personen in öffentlich zugänglichen Einrichtungen.
Zum Vergleich: Die amerikanische Verordnung ADA (Americans with Disabilities Act) schreibt ebenfalls ein maximales Verhältnis von 1:12 (also 8,33%) für öffentliche Zugangsrampen vor.
Topographie und Gelände
In der Topographie wird die Neigung zwischen zwei Messpunkten in verschiedenen Höhen berechnet. Die Höhenlinien auf IGN-Karten ermöglichen die Bestimmung des Gefälles (die Äquidistanz entspricht dem Höhenunterschied zwischen zwei Höhenlinien). Unser kleines Modul berechnet die tatsächliche Geländeneigung unter Berücksichtigung der Höhe.
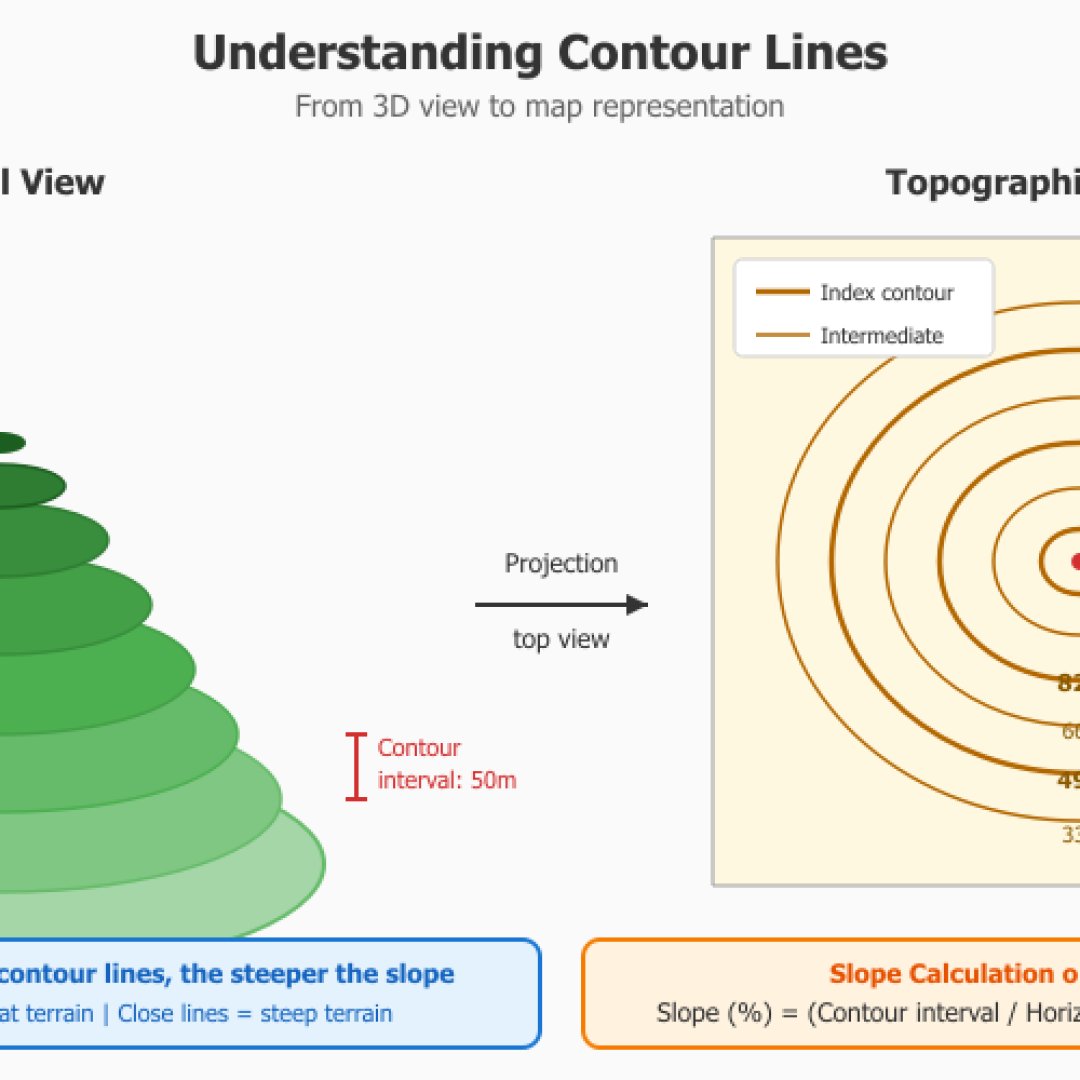
In der professionellen Topographie wird die Einheit Gon (oder Grad) oft bevorzugt, da sie den Kreis in 400 Teile unterteilt, was die Berechnungen vereinfacht (ein rechter Winkel = genau 100 Gon), hingegen drückt man sich im militärischen Bereich häufig in Strich im Heer und mehr in Grad auf NATO-Ebene aus.
Dachstuhl und Bau
Die Berechnung Ihres Holzdachstuhls hängt von der gewählten Neigung ab. Ein Dach mit einem oder zwei Gefällen benötigt Sparren, die je nach Neigung und Spannweite dimensioniert werden. Die Länge der Neigung (die der Hypotenuse entspricht) bestimmt die für Ihr Projekt benötigte Menge an Deckungsmaterialien.
Referenzformeln
Berechnung des Neigungsprozentsatzes
Neigung (%) = (Höhe / Horizontale Entfernung) × 100Umrechnung Prozent zu Grad
Winkel (°) = arctan(Neigung% / 100) × (180 / π)Umrechnung Grad zu Radiant
Radiant = Grad × (π / 180)Länge der Neigung (Satz des Pythagoras)
Länge = √(Höhe² + Entfernung²)Trigonometrische Beziehungen
tan(Winkel) = Höhe / Entfernung = Neigung% / 100
sin(Winkel) = Höhe / Hypotenuse
cos(Winkel) = Entfernung / HypotenuseUmrechnungen von Winkeleinheiten
Gon = Grad × (400 / 360)
NATO-Mil = Grad × (6400 / 360)
Bogenminuten = Grad × 60
Bogensekunden = Grad × 3600
Umdrehungen = Grad / 360
Milliradiant = Radiant × 1000Geradengleichung
Steigung-Achsenabschnitt-Form: y = mx + b
Punkt-Steigung-Form: y - y₁ = m(x - x₁)
Standardform: Ax + By = CLineare Regression (Methode der kleinsten Quadrate)
Steigung (m) = [n∑xy - ∑x∑y] / [n∑x² - (∑x)²]
Achsenabschnitt (b) = ȳ - m × x̄
Koeffizient R² = 1 - [∑(y - ŷ)² / ∑(y - ȳ)²]Euklidische Entfernung
Entfernung 2D = √[(x₂-x₁)² + (y₂-y₁)²]
Entfernung 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]Parallele und senkrechte Linien
Parallel: m₁ = m₂
Senkrecht: m₁ × m₂ = -1Winkeleinheiten: Referenzleitfaden
| Einheit | Symbol | Vollkreis | Hauptverwendung |
|---|---|---|---|
| Grad | ° | 360° | Geometrie, Bau, Navigation |
| Radiant | rad | 2π ≈ 6,283 | Mathematik, Physik, Ingenieurwesen |
| Gon | gon | 400 gon | Topographie, Geodäsie (Europa) |
| Umdrehung | turn | 1 turn | Programmierung (CSS), Robotik |
| Milliradiant | mrad | ~6283 mrad | Ballistik, Optik, Zielfernrohre |
| NATO-Mil | mil | 6400 mil | NATO-Militäranwendungen |
| Bogenminute | ′ | 21 600′ | Astronomie, Seenavigation |
| Bogensekunde | ″ | 1 296 000″ | Hochpräzision, GPS-Koordinaten |
Das Radiant ist die Winkeleinheit des Internationalen Systems (SI), definiert vom BIPM in der SI-Broschüre. Es entspricht dem Zentriwinkel, der einen Bogen von der Länge des Kreisradius abschneidet (Stellen Sie sich einen Kreis vor: Es ist der Zentriwinkel, der einen Bogen (einen Teil des Umfangs) von genau derselben Länge wie der Radius des Kreises ausschneidet. Es ist, als würden Sie den Radius entlang des Kreisrandes abrollen, um diesen Grundwinkel zu bilden!).
Häufig gestellte Fragen
Wie berechnet man eine Neigung in Prozent?
Sie teilen einfach die Höhe (Gefälle) durch die horizontale Entfernung. Dann multiplizieren Sie das Ganze mit 100. Zum Beispiel entsprechen 5 Meter Gefälle auf 50 Meter Entfernung 10% Neigung. Unser Tool ermöglicht es Ihnen, diese Berechnung automatisch durchzuführen.
Was ist der Unterschied zwischen Prozent und Grad?
Einerseits stellt der Prozentsatz ein Verhältnis dar, das der Höhe geteilt durch die Entfernung multipliziert mit 100 entspricht, und die Grad messen den geometrischen Winkel. Die Beziehung ist nicht linear. Das heißt, 100% entspricht 45 Grad. Aber 50% sind nicht 22,5 Grad. Tatsächlich sind es 26,6 Grad. Diese Nichtlinearität stammt von der Arkustangensfunktion (perfekt, um in Gesellschaft zu glänzen), die für die Umrechnung verwendet wird.
Wie berechnet man die Neigung eines Daches?
Sie müssen die Höhe des Firstes vom Niveau der Dachrinnen und die horizontale Entfernung bis zum Messpunkt messen. Dann verwenden Sie unseren Dachneigungsrechner, um den Prozentsatz zu erhalten und die Kompatibilität mit Ihrer Deckung zu überprüfen, seien es Ziegel, Schiefer oder Bleche.
Welche Neigung für ein Trapezblech-Dach?
Trapezblech akzeptiert flachere Neigungen, im Allgemeinen ab 5% (3 Grad), je nach DTU-Empfehlungen. Geringere Neigungen erfordern eine verstärkte Abdichtung für Ihr Projekt.
Referenz: NF DTU 40.35 - Deckung mit profilierten Platten aus beschichteten Stahlblechen (AFNOR).
Wie misst man eine Neigung im Gelände?
Ganz einfach. Falls Sie damit ausgestattet sind, verwenden Sie einen rotierenden Laserlevel, einen Neigungsmesser oder eine Smartphone-App mit Beschleunigungsmesser. Und für große Entfernungen nehmen Sie die Höhe an zwei Punkten auf, entweder mit einem GPS-System, das Ihnen eine Höhenmessung ermöglicht, oder berechnen Sie sie einfach von Ihrer Position aus einer topographischen Karte. Und Sie messen die zurückgelegte horizontale Entfernung.
Was ist der Koeffizient R² in der linearen Regression?
Der Bestimmtheitskoeffizient R² gibt den Anteil der Varianz der Daten an, der durch das lineare Modell erklärt wird. Ein R² von 0,95 bedeutet, dass 95% der Datenvariation durch die Regressionsgerade erklärt wird. Je näher R² bei 1 liegt, desto besser ist die Anpassung des Modells.
Warum unseren Rechner verwenden?
Unsere Neigungsberechnungssuite bietet Ihnen 8 komplementäre Module, die ein Maximum der bestehenden Bedürfnisse abdecken, von der einfachen Prozentberechnung bis zur fortgeschrittenen linearen Regression, die Kopfschmerzen bereitet. Die Benutzeroberfläche ermöglicht es Ihnen, Ihre Berechnungen einfach von Ihrem Mobiltelefon, Tablet oder Computer aus durchzuführen. Wissen Sie, dass alle Berechnungen von Ihrem Browser aus erfolgen, für maximale Geschwindigkeit und um totale Vertraulichkeit der von Ihnen übermittelten Daten zu gewährleisten.
Wir haben versucht, ein Maximum an Winkeleinheiten für alle verfügbar zu machen, am selben Ort (Grad, Radiant, Gon, Prozentsätze, Verhältnisse, Milliradiant, NATO-Mil, Bogen- und Bogensekunden und Umdrehungen). Normalerweise entsprechen sie den Bedürfnissen von Fachleuten im Bauwesen, der Topographie, Ballistik, Astronomie und fleißigen Schülern.
Berechnen Sie jetzt Ihre Neigung mit unseren kostenlosen Tools.