Online Hellingsberekening - Onze 8 Gratis Tools
Onze complete suite van hellingsberekeningen stelt u in staat om een helling te berekenen, of het nu in percentage, graden, radialen is, maar ook in alle bestaande hoek- en hellingseenheden. Of u nu de helling van uw dak, een oprit voor toegankelijkheid voor mensen met een beperking, uw terrein of een specifieke weg moet berekenen, onze tools dekken een breed spectrum van gebruikssituaties. Geen registratie vereist, de berekening wordt 100% client-side uitgevoerd, dus in uw browser, uw gegevens blijven privé.
Onze 8 berekeningsmodules
De basis hellingsberekening
Het maakt hellingsberekening mogelijk vanuit de hoogte en horizontale afstand, of direct vanuit een hoek als u deze kent. U voert uw hoogteverschil en afgelegde afstand in om het hellingspercentage evenals de hoek in graden, radialen, de verhouding en de lengte van de hypotenusa te verkrijgen.
De formule die gebruikt wordt is relatief eenvoudig, het gaat om het hellingspercentage dat gelijk is aan de hoogte gedeeld door de horizontale afstand vermenigvuldigd met 100: Helling (%) = (Hoogte / Horizontale afstand) × 100. Betreffende de hoek θ: θ = arctan(Hoogte / Afstand). De calculator categoriseert automatisch de helling, classificeert deze van zeer zacht tot extreem met voorbeelden van concrete toepassingen.
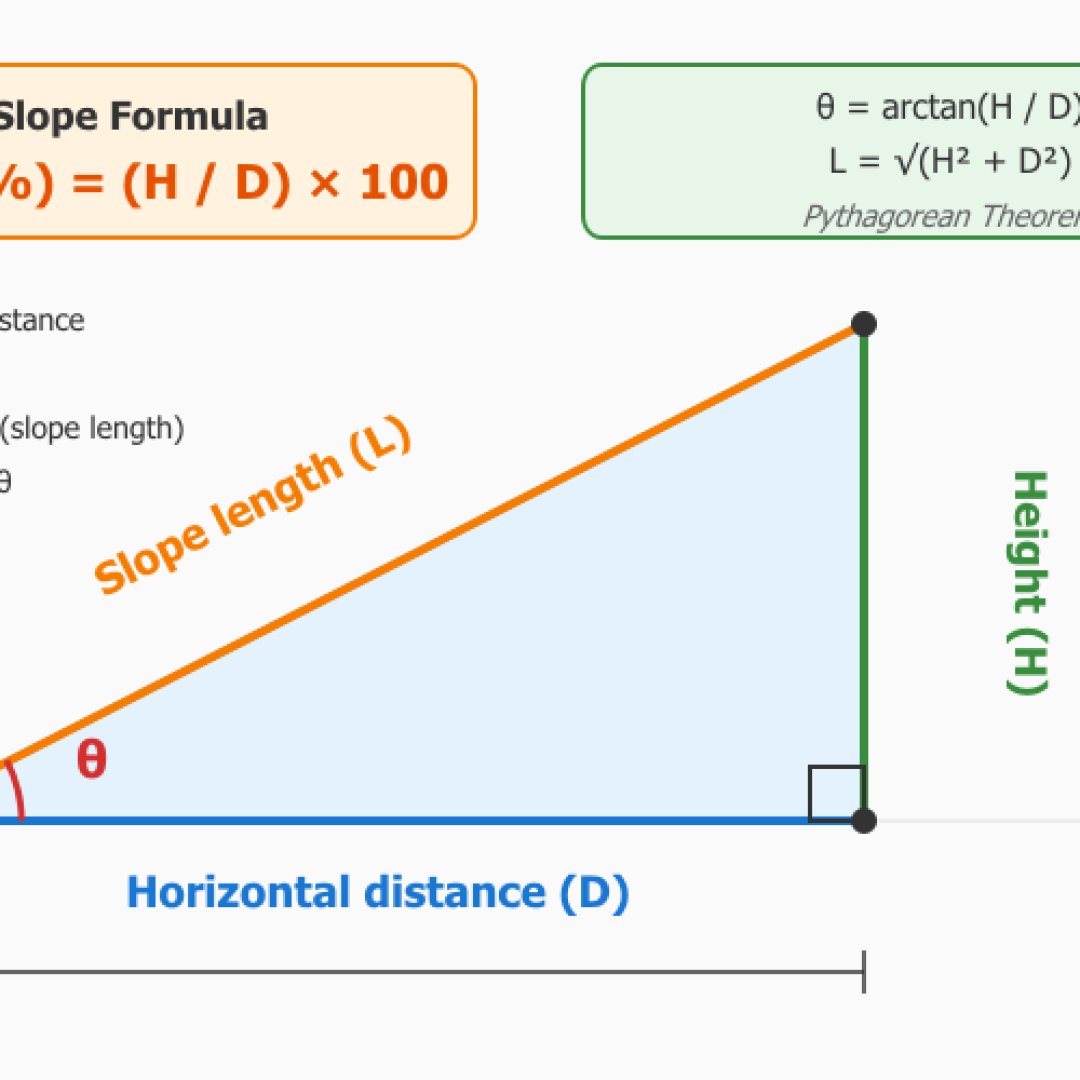
Deze module stelt u ook in staat om de omgekeerde berekening te maken. Dat wil zeggen, vanuit een bekende hoek en een dimensie (horizontale afstand, hoogte of hypotenusa), bepaalt het de twee andere ontbrekende dimensies dankzij fundamentele trigonometrische relaties.
De hoekeenheidsconverter
De hoekeenheidsconverter is compleet en stelt u in staat om direct van de ene eenheid naar de andere over te gaan. Het ondersteunt 10 soorten eenheden, of het nu percentage, graden, radialen, gradianen (gebruikt in topografie), toeren (bijvoorbeeld gebruikt in CSS), milliradialen (ballistiek), NATO mils (militair), boogminuten en boogseconden (astronomie), en de verhouding (1:X) betreft.
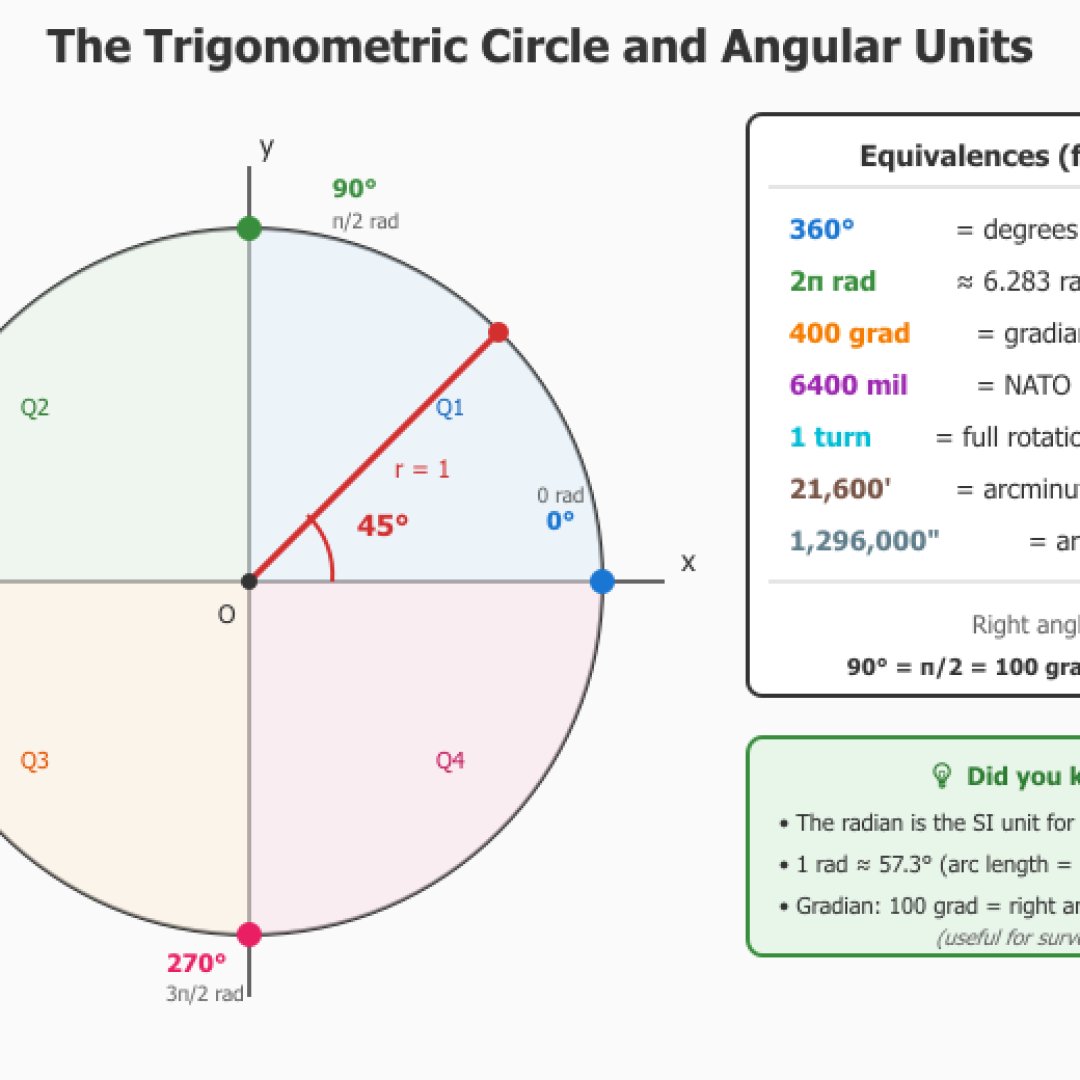
De dynamische visualisatie toont u de trigonometrische cirkel evenals de hellingsdriehoek om visueel de relatie tussen de hoek en de helling te begrijpen. Opmerkelijke hoeken worden automatisch gedetecteerd (normaal gesproken ^^) en tonen hun notatie in π (bijvoorbeeld π/4 rad voor 45°).
De afstands- en middelpuntberekening
Deze module maakt het mogelijk om de Euclidische afstand tussen twee punten in twee dimensies of in drie dimensies te berekenen. Betreffende de driedimensionale berekening, bepaalt het ook de helling van het terrein tussen twee hoogtes, wat nuttig kan zijn in topografie evenals bij wandelen.
De formules zijn gebaseerd op de stelling van Pythagoras, bewezen in Euclides' Elementen (Boek I, Propositie 47):
- Afstand 2D = √[(x₂-x₁)² + (y₂-y₁)²]
- Afstand 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]
- Middelpunt = ((x₁+x₂)/2, (y₁+y₂)/2)
De 3D-module berekent ook de richtingshoeken van de verplaatsingsvector ten opzichte van de drie assen X, Y en Z, wat nuttig kan zijn in topografie en navigatie maar eerlijk gezegd is het vooral nuttig op school!
Lijnvergelijking (y = mx + b)
Maakt het mogelijk om de vergelijking van een rechte lijn te genereren vanuit twee punten of vanuit een helling en een punt. Deze module biedt drie soorten vormen: de helling-snijpunt vorm (y = mx + b), de punt-helling vorm (y - y₁ = m(x - x₁)) evenals de standaardvorm (Ax + By = C). Het stelt u in staat om het x-snijpunt, y-snijpunt te berekenen en eenvoudig te controleren of drie punten collineair zijn.
De collineariteit wordt gecontroleerd door de berekening van de oppervlakte van de driehoek gevormd door de drie punten. Als de oppervlakte nul is, zijn de punten dan uitgelijnd.
De interactieve grafische visualisatie
Door gebruik te maken van een grafiek met de Chart.js bibliotheek, maakt het het mogelijk om uw lijnen en punten te tekenen. U voegt lijnen toe per vergelijking of coördinaten. U controleert de zoom van ±5 tot ±100. U activeert en deactiveert de rasters. En u kunt het resultaat exporteren in PNG-afbeelding of in vectorieel SVG-formaat dat het mogelijk maakt om geen kwaliteit te verliezen bij vergroting.
Parallelle en loodrechte lijnen
Stellen u in staat om de vergelijking van een parallelle of loodrechte lijn te vinden die door een gegeven punt gaat. De wiskundige regels zijn als volgt: twee lijnen zijn parallel als m₁ = m₂, loodrecht als m₁ × m₂ = -1. De geïntegreerde verificator analyseert de bestaande relatie tussen twee hellingen en berekent de hoek gevormd tussen twee snijdende rechte lijnen.
Deze eigenschappen vloeien direct voort uit de Euclidische meetkunde, fundamentele begrippen in analytische meetkunde voor de studie van rechte lijnen in het Cartesiaanse vlak.
Lineaire regressie
Stelt u in staat om de trendlijn te berekenen met de kleinste kwadraten methode door uw gegevens handmatig in te voeren, door ze te plakken of te importeren via een CSV-bestand. De module berekent de correlatiecoëfficiënt R, de determinatiecoëfficiënt R² evenals de standaardfout en de residuen. Zo kunt u voorspellingen maken van Y voor gegeven X.
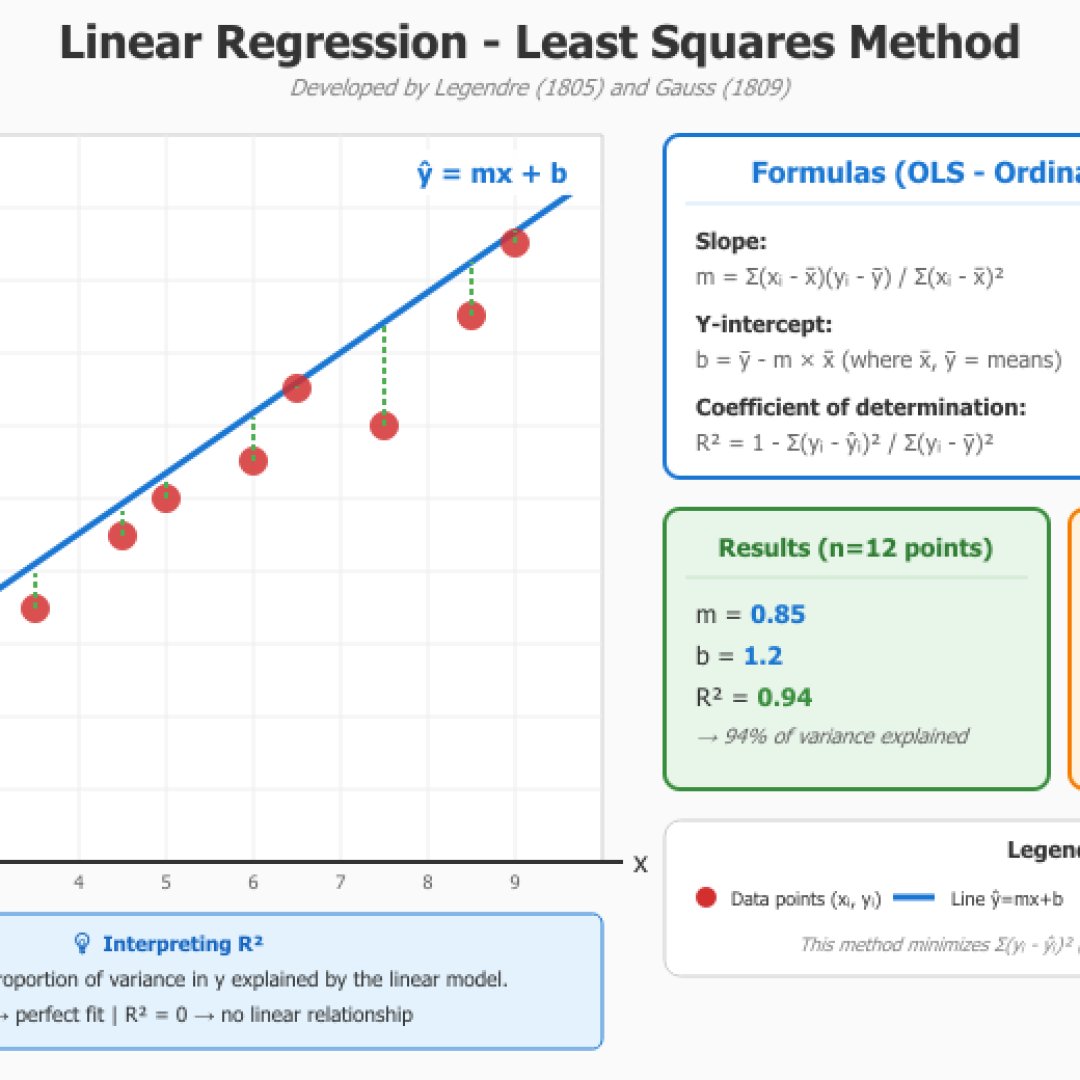
De kleinste kwadraten methode werd ontwikkeld door Adrien-Marie Legendre (1805) en Carl Friedrich Gauss (1809), het minimaliseert de som van de kwadraten van de afwijkingen tussen de waargenomen waarden en de waarden voorspeld door het lineaire model.
Hoeken en elevatie
U berekent elevatie- en depressiehoeken voor uw projecten, of het nu gaat om ballistische schietsport, het richten van uw telescopen naar de sterren, het berekenen van een klimhoek in een vliegtuig of de berekening van een oprithoek voor uw bouwactiviteiten. De omgekeerde berekening maakt het mogelijk om de ontbrekende afstand of hoogte te vinden vanuit een bekende hoek.
Deze module accepteert de invoerhoek in de 10 ondersteunde eenheden, inclusief direct in hellingspercentage.
Hellingsberekening eenvoudig begrijpen
De helling in percentage
Het hellingspercentage vertegenwoordigt de verhouding die bestaat tussen het hoogteverschil en de horizontale afstand, het geheel vermenigvuldigd met 100. Een helling van 10% betekent dan dat voor 100 meter horizontale afstand, u 10 meter hoogte wint. Dit is het standaardformaat dat gebruikt wordt op verkeersborden en in de bouw.
De helling in graden
De hoek van de helling meet de helling ten opzichte van de horizontaal. Zo komt een hoek van 45 graden overeen met een helling van 100% (hoogte gelijk aan afstand). De conversie gebruikt de tangensfunctie: % = tan(hoek) × 100.
Gangbare overeenkomsten
| Percentage | Hoek | Typisch gebruik |
|---|---|---|
| 5% | 2.9° | Toegankelijkheidsoprit (wettelijk maximum) |
| 10% | 5.7° | Fietspad, oprijlaan |
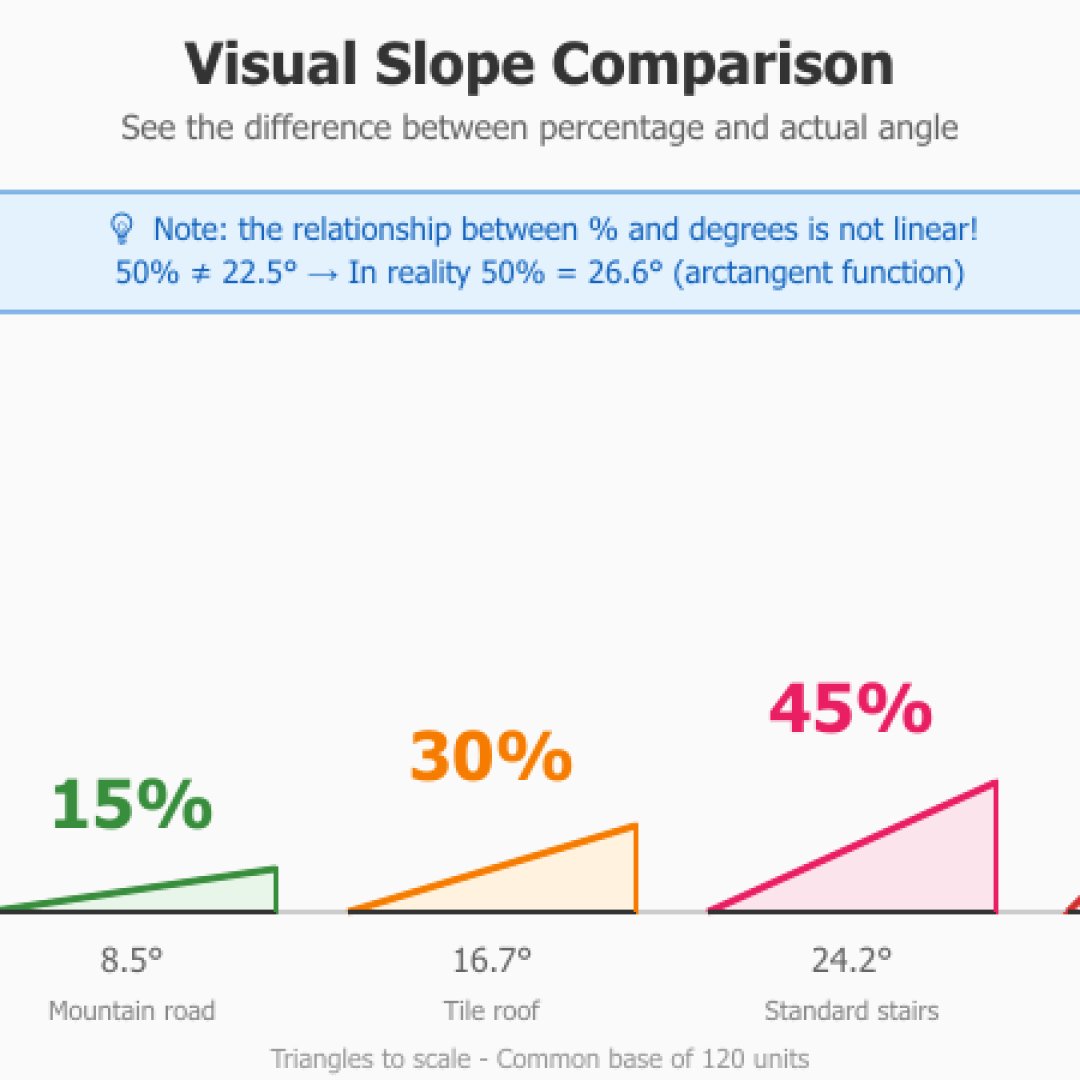
| 15% | 8.5° | Bergweg |
| 30% | 16.7° | Zachte trap, dak met lage helling |
| 45% | 24.2° | Standaard trap |
| 100% | 45° | Maximaal begaanbare helling |
Praktische toepassingen
Dakhellingberekening
De helling van het dak beïnvloedt noodzakelijkerwijs de keuze van dakbedekkingsmaterialen evenals de afvoer van regenwater. Platte daken vereisen over het algemeen minimaal 5% om de afvoer van regenwater te verzekeren. Pannendaken vragen gewoonlijk 15 tot 35% afhankelijk van het type pannen (mechanische pannen, gootpannen of leien). Besneeuwde berggebieden vereisen steilere hellingen van 35% tot 60% om te voorkomen dat daken in de winter instorten onder het gewicht van de sneeuw.
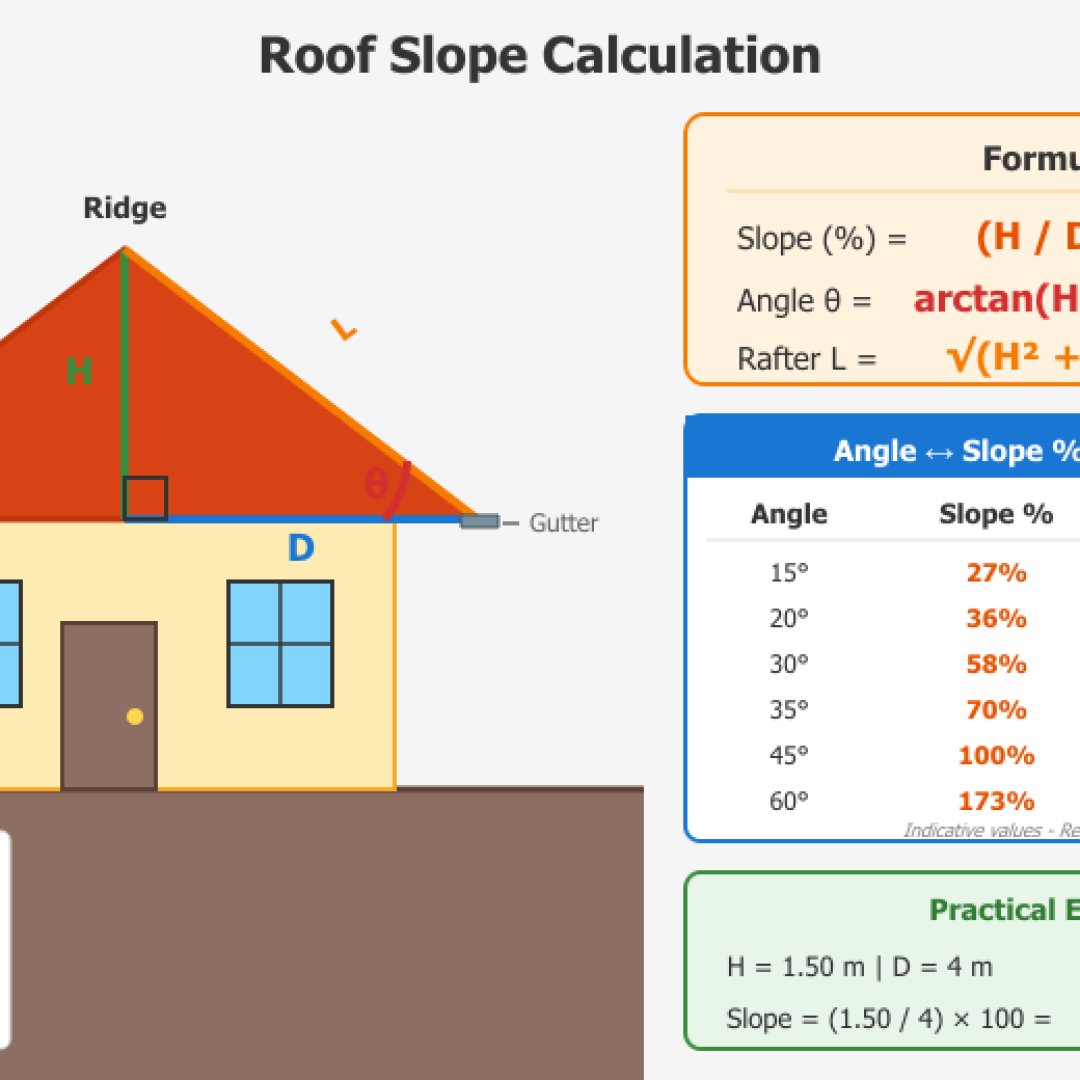
Om de helling van uw dak te berekenen, moet u dus de hoogte van de gevel meten en de horizontale afstand (de halve breedte van het gebouw voor een zadeldak). Onze kleine dakhellingcalculator geeft het resultaat in percentage en in graden.
De oprit voor personen met beperkte mobiliteit en toegankelijkheid
De Franse regelgeving legt een maximale helling van 5% op voor toegangsopritten voor personen met beperkte mobiliteit. Echter, uitzonderingen staan tot 8% toe over maximaal 2 meter of 10% over 50 cm. Onze calculator maakt het mogelijk om de conformiteit van uw toegankelijkheidsverbeteringsproject te controleren.
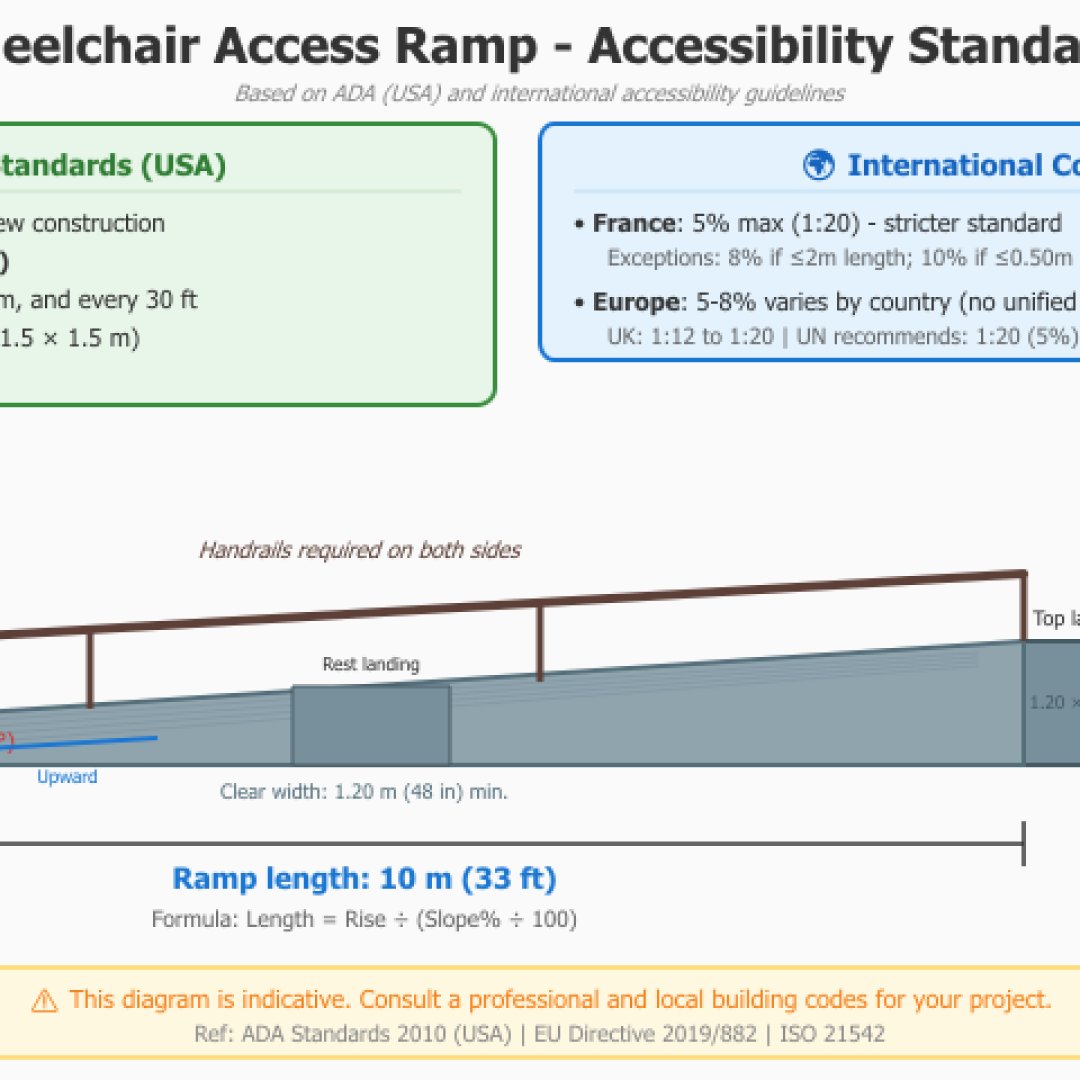
Referentie: Besluit van 20 april 2017 betreffende de toegankelijkheid voor gehandicapten van openbare gebouwen.
Ter vergelijking legt de Amerikaanse ADA (Americans with Disabilities Act) regelgeving ook een maximale verhouding van 1:12 (dat is 8.33%) op voor openbare toegangsopritten.
Topografie en terrein
In topografie wordt de helling berekend tussen twee meetpunten op verschillende hoogtes. De hoogtelijnen op IGN-kaarten maken het mogelijk om het hoogteverschil te bepalen (de equidistantie is gelijk aan het hoogteverschil tussen twee hoogtelijnen). Onze kleine module berekent de werkelijke helling van het terrein rekening houdend met de hoogte.
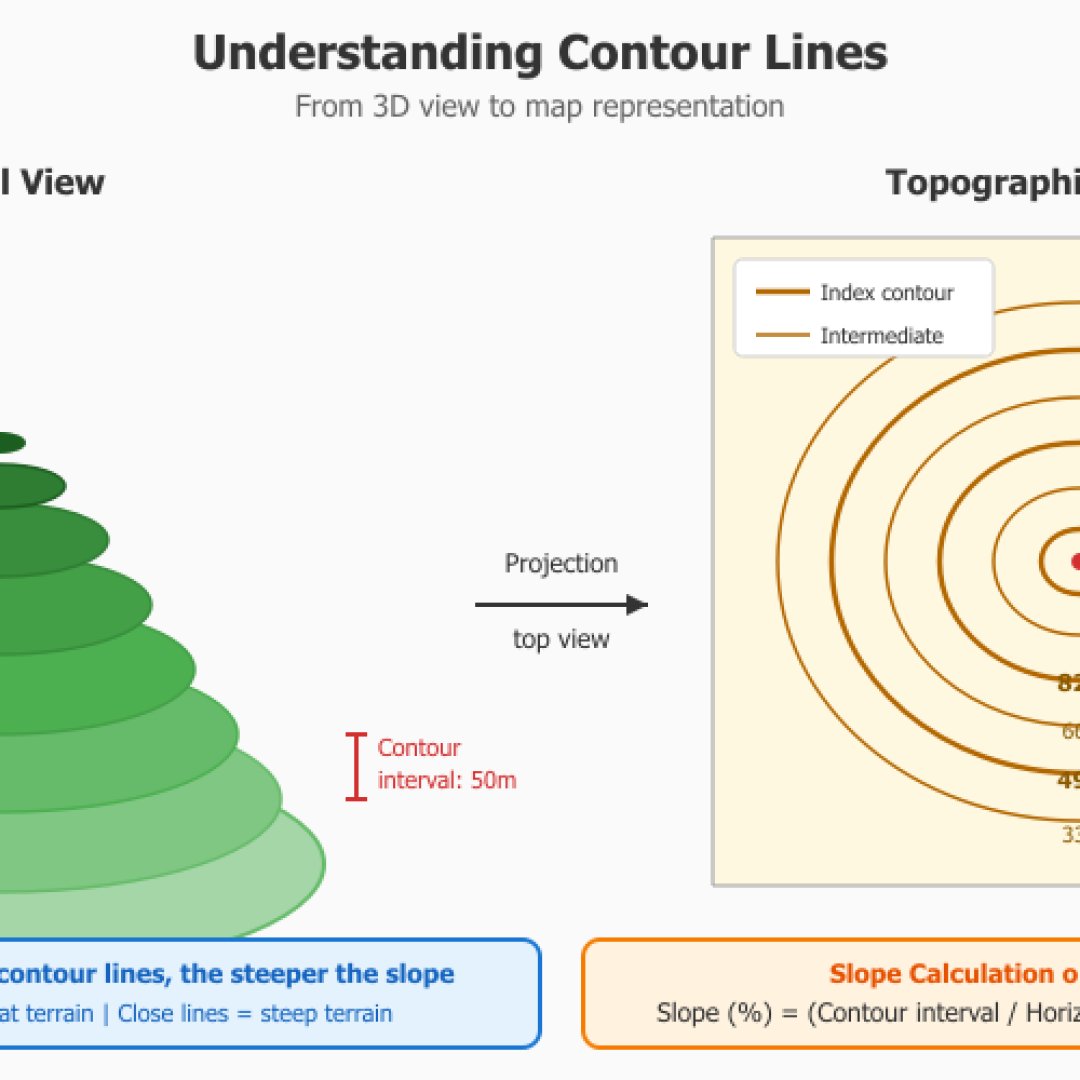
In professionele topografie wordt de gradiaan (of gon) eenheid vaak verkozen omdat het de cirkel verdeelt in 400 delen, wat de berekeningen vereenvoudigt (een rechte hoek = precies 100 grad), daarentegen in militaire context drukt men zich vaak uit in duizendsten in het landleger en meer in graden op NAVO-niveau.
Dakconstructie en bouw
De berekening van uw houten dakconstructie hangt af van de gekozen helling. Een dak bestaande uit één of twee hellingen vereist spanten die gedimensioneerd worden volgens de helling en de overspanning. De lengte van de helling (die overeenkomt met de hypotenusa) bepaalt de hoeveelheid dakbedekkingsmaterialen die nodig zijn voor uw project.
Referentieformules
Berekening van hellingspercentage
Helling (%) = (Hoogte / Horizontale afstand) × 100Conversie percentage naar graden
Hoek (°) = arctan(Helling% / 100) × (180 / π)Conversie graden naar radialen
Radialen = Graden × (π / 180)Lengte van de helling (stelling van Pythagoras)
Lengte = √(Hoogte² + Afstand²)Trigonometrische relaties
tan(hoek) = Hoogte / Afstand = Helling% / 100
sin(hoek) = Hoogte / Hypotenusa
cos(hoek) = Afstand / HypotenusaConversies van hoekeenheden
Gradianen = Graden × (400 / 360)
Mils NATO = Graden × (6400 / 360)
Boogminuten = Graden × 60
Boogseconden = Graden × 3600
Toeren = Graden / 360
Milliradialen = Radialen × 1000Lijnvergelijking
Helling-snijpunt vorm: y = mx + b
Punt-helling vorm: y - y₁ = m(x - x₁)
Standaardvorm: Ax + By = CLineaire regressie (kleinste kwadraten methode)
Helling (m) = [n∑xy - ∑x∑y] / [n∑x² - (∑x)²]
Y-snijpunt (b) = ȳ - m × x̄
Coëfficiënt R² = 1 - [∑(y - ŷ)² / ∑(y - ȳ)²]Euclidische afstand
Distance 2D = √[(x₂-x₁)² + (y₂-y₁)²]
Distance 3D = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]Parallelle en loodrechte lijnen
Parallel: m₁ = m₂
Loodrecht: m₁ × m₂ = -1Hoekeenheden: referentiegids
| Eenheid | Symbool | Volledige cirkel | Hoofdgebruik |
|---|---|---|---|
| Graad | ° | 360° | Meetkunde, bouw, navigatie |
| Radiaal | rad | 2π ≈ 6.283 | Wiskunde, natuurkunde, techniek |
| Gradiaan | grad | 400 grad | Topografie, geodesie (Europa) |
| Toer | turn | 1 turn | Programmering (CSS), robotica |
| Milliradiaal | mrad | ~6283 mrad | Ballistiek, optica, richtkijkers |
| Mil NATO | mil | 6400 mil | Militaire NAVO-toepassingen |
| Boogminuut | ′ | 21 600′ | Astronomie, zeevaart |
| Boogseconde | ″ | 1 296 000″ | Hoge precisie, GPS-coördinaten |
De radiaal is de hoekeenheid van het Internationale Systeem (SI), gedefinieerd door het BIPM in de SI-brochure. Het komt overeen met de middelpuntshoek die een boog onderschept met een lengte gelijk aan de straal van de cirkel (Stel je een cirkel voor: het is de middelpuntshoek die een boog (een deel van de omtrek) afsnijdt van precies dezelfde lengte als de straal van de cirkel. Het is alsof je de straal langs de rand van de cirkel afrolt om deze basishoek te vormen!).
Veelgestelde vragen
Hoe bereken je een helling in percentage?
U deelt eenvoudig de hoogte (hoogteverschil) door de horizontale afstand. Vervolgens vermenigvuldigt u het geheel met 100. Bijvoorbeeld, 5 meter hoogteverschil over 50 meter afstand komt overeen met 10% helling. Onze tool stelt u in staat om deze berekening automatisch uit te voeren.
Wat is het verschil tussen een percentage en graden?
Enerzijds vertegenwoordigt het percentage een verhouding die overeenkomt met de hoogte gedeeld door de afstand vermenigvuldigd met 100, en graden meten de geometrische hoek. De relatie is niet lineair. Dat wil zeggen dat 100% gelijk is aan 45 graden. Maar 50% zal niet 22,5 graden zijn. In werkelijkheid is het 26,6 graden. Deze niet-lineariteit komt voort uit de arctangensfunctie (perfect om te schitteren in gezelschap) die gebruikt wordt voor de conversie.
Hoe bereken je de helling van een dak?
U moet de hoogte van de nok meten vanaf het niveau van de dakgoten en de horizontale afstand tot het meetpunt. Gebruik vervolgens onze dakhellingcalculator om het percentage te verkrijgen en de compatibiliteit met uw dakbedekking te controleren, of het nu pannen, leien of platen betreft.
Welke helling voor een stalen plaatdak?
Staalplaat accepteert lagere hellingen, gewoonlijk vanaf 5% (3 graden), volgens DTU-aanbevelingen. Lagere hellingen vereisen versterkte waterdichting voor uw project.
Referentie: NF DTU 40.35 - Dakbedekking in geribbelde platen van gecoate staalplaten (AFNOR).
Hoe meet je een helling op het terrein?
Heel eenvoudig. Als u ermee uitgerust bent, gebruikt u een roterende laser waterpas, een clinometer of een smartphone-app met een accelerometer. En voor grote afstanden noteert u de hoogte op twee punten, hetzij met een GPS-systeem dat u in staat stelt om een hoogtemeting te doen, of eenvoudig berekent u het vanaf uw positie vanaf een topografische kaart. En u meet de afgelegde horizontale afstand.
Wat is de R²-coëfficiënt in lineaire regressie?
De determinatiecoëfficiënt R² geeft de proportie van de variantie van de gegevens aan die verklaard wordt door het lineaire model. Een R² van 0.95 betekent dat 95% van de variatie van de gegevens verklaard wordt door de regressielijn. Hoe dichter R² bij 1 ligt, hoe beter de aanpassing van het model.
Waarom onze calculator gebruiken?
Onze suite van hellingsberekeningen biedt u 8 complementaire modules die een maximum van bestaande behoeften dekken, van eenvoudige percentageberekening tot geavanceerde lineaire regressie die hoofdpijn veroorzaakt. De interface stelt u in staat om uw berekeningen eenvoudig uit te voeren vanaf uw mobiele telefoon, tablet of computer. Weet dat alle berekeningen uitgevoerd worden vanaf uw browser, voor maximale snelheid en om totale vertrouwelijkheid van de gegevens die u indient te garanderen.
We hebben geprobeerd om een maximum aan hoekeenheden beschikbaar te stellen voor iedereen, op dezelfde plaats (graden, radialen, gradianen, percentages, verhoudingen, milliradialen, NATO mils, boog- en seconden en toeren). Normaal gesproken beantwoorden ze aan de behoeften van professionals in de bouw, topografie, ballistiek, astronomie en van studieuse leerlingen.
Bereken nu uw helling met onze gratis tools.